题目内容
17. 将一副三角板按如图所示的方式叠放,则角α=75°.
将一副三角板按如图所示的方式叠放,则角α=75°.
分析 根据平行线的性质得到∠ACD=∠CDB=30°,根据三角形的外角的性质计算即可.
解答 解: 由题意得,∠ACB=∠CBD=90°,
由题意得,∠ACB=∠CBD=90°,
∴AC∥BD,
∴∠ACD=∠CDB=30°,
∴α=45°+30°=75°,
故答案为:75°.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
5.点P的坐标为(-1,2),则点P位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.点P(a-2,2a+3)到两坐标轴的距离相等,则点P的坐标为( )
| A. | (-7,-7) | B. | (-$\frac{7}{3}$,$\frac{7}{3}$) | C. | (-7,-7)或(-$\frac{7}{3}$,$\frac{7}{3}$) | D. | (-7,-7)或($\frac{7}{3}$,-$\frac{7}{3}$) |
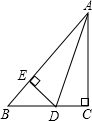 如图,△ABC中,∠C=90°,BC=9,AD平分∠BAC,过点D作DE⊥AB于E,测得BE=3,则△BDE的周长是( )
如图,△ABC中,∠C=90°,BC=9,AD平分∠BAC,过点D作DE⊥AB于E,测得BE=3,则△BDE的周长是( )