题目内容
已知,一抛物线经过点(0,-1),(1,-2),(-2,7),求其解析式及其顶点坐标.
考点:待定系数法求二次函数解析式
专题:计算题
分析:先设一般式y=ax2+bx+c,再把三个点的坐标代入得到关于a、b、c的方程组,解方程组求出a、b、c的值即可得到抛物线解析式,然后配成顶点式得到顶点坐标.
解答:解:设抛物线解析式为y=ax2+bx+c,
根据题意得
,解得
,
所以抛物线解析式为y=x2-2x-1,
因为y=x2-2x-1=(x-1)2-2,
所以抛物线顶点坐标为(1,-2).
根据题意得
|
|
所以抛物线解析式为y=x2-2x-1,
因为y=x2-2x-1=(x-1)2-2,
所以抛物线顶点坐标为(1,-2).
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
如果一个多项式的次数是5,那么这个多项式的任何一项的次数满足( )
| A、都小于5 | B、都大于5 |
| C、都不小于5 | D、都不大于5 |
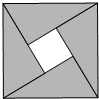 如图是我国古代数学家赵爽的“勾股方圆图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是12,小正方形的面积是2,直角三角形的两直角边分别是a和b,求(a+b)2的值.
如图是我国古代数学家赵爽的“勾股方圆图”,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是12,小正方形的面积是2,直角三角形的两直角边分别是a和b,求(a+b)2的值. 在△ABC中,∠C=30°,cosB=
在△ABC中,∠C=30°,cosB= 如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第
如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第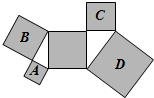 如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为
如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,已知正方形A、B、C的面积依次为2、4、3,则正方形D的面积为