题目内容
 如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.考点:等边三角形的性质
专题:
分析:先根据△ABC是等边三角形,AD为中线可得出AD⊥BC,∠CAD=30°,再由AD=AE可知∠ADE=∠AED,根据三角形内角和定理即可求出∠ADE的度数,故可得出∠EDC的度数.
解答:解:∵△ABC是等边三角形,AD为中线,
∴AD⊥BC,∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=
=
=75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
∴AD⊥BC,∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=
| 180°-∠CAD |
| 2 |
| 180°-30° |
| 2 |
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
点评:本题考查的是等边三角形的性质及等腰三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目

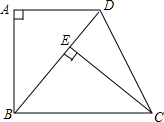 如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E. 有一块锐角三角形木料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为2cm和1cm的小长方形零件,分割方式如图所示,使最底层的小方形的长为2cm的边在BC上,一层一层往上分割,分割线的耗料不计,则按如图方式分割成的小长方形零件最多有
有一块锐角三角形木料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为2cm和1cm的小长方形零件,分割方式如图所示,使最底层的小方形的长为2cm的边在BC上,一层一层往上分割,分割线的耗料不计,则按如图方式分割成的小长方形零件最多有