题目内容
 有一块锐角三角形木料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为2cm和1cm的小长方形零件,分割方式如图所示,使最底层的小方形的长为2cm的边在BC上,一层一层往上分割,分割线的耗料不计,则按如图方式分割成的小长方形零件最多有
有一块锐角三角形木料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为2cm和1cm的小长方形零件,分割方式如图所示,使最底层的小方形的长为2cm的边在BC上,一层一层往上分割,分割线的耗料不计,则按如图方式分割成的小长方形零件最多有考点:相似三角形的应用
专题:
分析:如图作EF交BA、BC于点E、F,得到EF∥BC,利用相似三角形求得GD的长,进而可以求得可以裁几层这样的长方形,从而得到答案.
解答: 解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,
解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,
EF∥BC,
∴△AEF∽△ABC,
∴
=
,
∵BC=12cm,AD=9cm,小正方形邻边长分别为2cm和1cm
∴
=
解得:AG=1.5,
∴GD=7.5cm,
∵小正方形的宽为1cm,
∴能分割7层小长方形,
同理可得出:最下面一层可分割成5个长方形,
其次分割成4个长方形,再上一层分割成4个长方形,
再上一层分割成3个长方形,再上一层分割成2个长方形,
再上一层分割成2个长方形,最上一层分割成1个长方形,
故共裁21个小长方形.
故答案为:21.
 解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,
解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,EF∥BC,
∴△AEF∽△ABC,
∴
| EF |
| BC |
| AG |
| AD |
∵BC=12cm,AD=9cm,小正方形邻边长分别为2cm和1cm
∴
| 2 |
| 12 |
| AG |
| 9 |
解得:AG=1.5,
∴GD=7.5cm,
∵小正方形的宽为1cm,
∴能分割7层小长方形,
同理可得出:最下面一层可分割成5个长方形,
其次分割成4个长方形,再上一层分割成4个长方形,
再上一层分割成3个长方形,再上一层分割成2个长方形,
再上一层分割成2个长方形,最上一层分割成1个长方形,
故共裁21个小长方形.
故答案为:21.
点评:本题考查了相似三角形的应用,利用条件得到相似三角形并利用相似三角形的性质求得每层长方形个数是解决本题的关键.

练习册系列答案
相关题目
 如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数. 电脑设计了这样一个运算程序如图,请问当输入的数值是-3时,最后输出的结果是
电脑设计了这样一个运算程序如图,请问当输入的数值是-3时,最后输出的结果是 如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连结EC,则∠ECD的度数是
如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连结EC,则∠ECD的度数是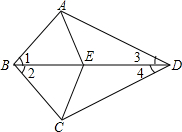 已知:如图,∠1=∠2,∠3=∠4,点E在BD上,连结AE、CE,求证:AE=CE.
已知:如图,∠1=∠2,∠3=∠4,点E在BD上,连结AE、CE,求证:AE=CE.