题目内容
如图，AB∥DE，∠B=140°，∠D=150°，则∠C=考点：平行线的性质
专题：
分析：过C作CF∥AB，根据平行线的性质可得到∠B+∠BCF=∠D+∠DCF=180°，可求得∠BCD．
解答：
解：如图，过点C作CF∥AB，
∵AB∥DE，
∴CF∥DE，
∴∠B+∠BCF=∠D+∠DCF=180°，
∴∠BCF=180°-∠B=180°-140°=40°，∠DCF=180°-∠D=180°-150°=30°，
∴∠BCD=∠BCF+∠DCF=40°+30°=70°．
故答案为：70°．
解：如图，过点C作CF∥AB，∵AB∥DE，
∴CF∥DE，
∴∠B+∠BCF=∠D+∠DCF=180°，
∴∠BCF=180°-∠B=180°-140°=40°，∠DCF=180°-∠D=180°-150°=30°，
∴∠BCD=∠BCF+∠DCF=40°+30°=70°．
故答案为：70°．
点评：本题主要考查平行线的性质，掌握平行线的性质是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补．
练习册系列答案
核心素养学练评系列答案
相关题目
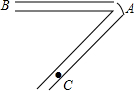工人李师傅想制作一个如图所示的“V”形零件，他先把材料变成一个40°的锐角，然后准备在C处第二次加工拐弯，请你帮助他算一下，他应该怎样向外弯才能保证变过来的部分与AB保持平行？你的依据是什么？
你能利用平行线的有关知识来说明“三角形的内角和等于180°”吗？
如图，已知EB∥DC，∠C=∠E，∠A=40°，点A，B，C三点共线，求∠ADE的度数．