题目内容
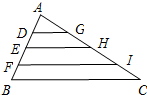 如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=2a,则DG+EH+FI的长是( )
如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=2a,则DG+EH+FI的长是( )A、
| ||
| B、4a | ||
| C、3a | ||
D、
|
考点:平行线分线段成比例
专题:
分析:由于D、E、F和G、H、I分别是AB、AC的四等分点,则DG∥EH∥FI,根据平行线分线段成比例定理,即可求出DG、EH、FI和BC的比例关系,由此可求出DG+EH+FI的长.
解答:解:∵AD=DE=EF=FB,AG=GH=HI=IC,
∴DG∥EH∥FI;
∴
=
,即DG=
BC;
同理可得:EH=
BC,FI=
BC;
∴DG+EH+FI=
BC+
BC+
BC=
BC=3a;
故选C.
∴DG∥EH∥FI;
∴
| AD |
| AB |
| DG |
| BC |
| 1 |
| 4 |
同理可得:EH=
| 1 |
| 2 |
| 3 |
| 4 |
∴DG+EH+FI=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
故选C.
点评:此题主要考查的是平行线分线段成比例定理的应用,找准对应关系,避免错选其它答案.

练习册系列答案
相关题目
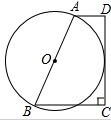 如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.
如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O. 如图,D、E分别是△ABC的边AC、AB上的点,AE=6,AC=10,BC=15,且
如图,D、E分别是△ABC的边AC、AB上的点,AE=6,AC=10,BC=15,且 如图是一个正方体盒子的展开图,要把-8、10、-12、8、-10、12些数字分别填入六个小正方形,使得按虚线折成的正方体相对面上的两个数相加得0.
如图是一个正方体盒子的展开图,要把-8、10、-12、8、-10、12些数字分别填入六个小正方形,使得按虚线折成的正方体相对面上的两个数相加得0.