题目内容
11.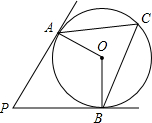 如图,PA,PB是圆O的两条切线,A,B分别是切点,点C是优弧AB上任意一点,连结OA,OB,CA,CB,∠P=60°,则∠ACB=60度.
如图,PA,PB是圆O的两条切线,A,B分别是切点,点C是优弧AB上任意一点,连结OA,OB,CA,CB,∠P=60°,则∠ACB=60度.
分析 由PA与PB都为圆O的切线,利用切线的性质得到OA与AP垂直,OB与BP垂直,在四边形APBO中,根据四边形的内角和求出∠AOB的度数,再利用同弧所对的圆周角等于所对圆心角的一半求出∠ACB的度数即可.
解答 解:∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°,
又∵∠P=60°,
∴∠AOB=360°-(∠OAP+∠OBP+∠P)=120°,
∵圆周角∠ADB与圆心角∠AOB都对弧AB,
∴∠ACB=$\frac{1}{2}$∠AOB=60°,
故答案为:60.
点评 此题考查了切线的性质,圆周角定理以及四边形的内角和,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
11.下列命题中的真命题是( )
| A. | 菱形是中心对称图形,但不是轴对称图形 | |
| B. | 相等的弦所对应的弦心距相等 | |
| C. | 直角三角形的外心和重心之间的距离等于斜边的六分之一 | |
| D. | 三角形的内心是三角形三边的中垂线的交点 |
6.下列说法错误的是( )
| A. | 平分弦的直径垂直于弦 | B. | 半圆(或直径)所对的圆周角是直角 | ||
| C. | 相等的圆心角所对的弧相等 | D. | 垂直半径的一端的直线是圆的切线 |
16. 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{4\sqrt{13}}{13}$ |
20.25的平方根是( )
| A. | ±5 | B. | -5 | C. | 5 | D. | 25 |
1.等腰直角三角形的斜边长为a,则其斜边上的高为( )
| A. | $\frac{a}{2}$ | B. | $\sqrt{2}a$ | C. | $\frac{\sqrt{3}}{2}$a | D. | $\frac{\sqrt{2}}{4}$a |
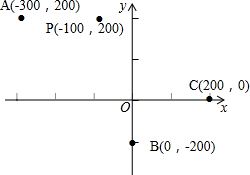 某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,1个单位长度为100km,地震监测部门测得该地区发生过一次地震,震中位置为P(-100,200),影响范围的半径为300km,如图所示,主干线沿线附近有3个城市:A(-300,200),B(0,-100),C(200,0),问在地震中受影响的是哪些城市?为什么?
某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,1个单位长度为100km,地震监测部门测得该地区发生过一次地震,震中位置为P(-100,200),影响范围的半径为300km,如图所示,主干线沿线附近有3个城市:A(-300,200),B(0,-100),C(200,0),问在地震中受影响的是哪些城市?为什么?