��Ŀ����
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=| 1 |
| 2 |
��1���ֱ����߶�OB��OC�ij���
��2����P��x��Ĵ��ߣ���ֱ��AB�ڵ�Q����Q��x���ƽ���߽�ֱ��CD�ڵ�M�����߶�QM�ij�Ϊy����-6��t��4ʱ����y��t�ĺ�����ϵʽ��
��3������TΪֱ��CD��һ���㣬����O��B��TΪ���������������O��B��PΪ���������������ʱ������Ӧ�ĵ�P��t��0�������꣮
���㣺һ�κ����ۺ���
ר�⣺
��������1�������Ա�����ֵ���ɵ���Ӧ�ĺ���ֵ����OB�ij��ȣ����ݴ���ϵ�������ɵ�CD�Ľ���ʽ�����ݺ���ֵ���ɵ���Ӧ�Ա�����ֵ��
��2���������ۣ�-6��t��2��2��t��2������QM��x�ᣬ�ɵ�Q��M����������ȣ����ݴ�ĺ������С�ĺ����꣬�ɵô𰸣�
��3���������ۣ��ٵ�C��T�غ�ʱ���ɵá�P1OB�ס�TOB����P2OB�ס�BOT���ڵ�C��T���غ�ʱ����P1OB�ס�TOB����P4OB�ס�OBT���������������ε����ʣ��ɵô𰸣�
��2���������ۣ�-6��t��2��2��t��2������QM��x�ᣬ�ɵ�Q��M����������ȣ����ݴ�ĺ������С�ĺ����꣬�ɵô𰸣�
��3���������ۣ��ٵ�C��T�غ�ʱ���ɵá�P1OB�ס�TOB����P2OB�ס�BOT���ڵ�C��T���غ�ʱ����P1OB�ס�TOB����P4OB�ס�OBT���������������ε����ʣ��ɵô𰸣�
����⣺��1����x=0ʱ��y=3��B��0��3��
��OB=3��
D��DE��x���ڵ�E��2��0������
D��������2��
��x=2ʱ��y=
��2+3=4����D�������ǣ�2��4����
ֱ��CD y=kx+8����D��2��4������
2k+8=4��
���k=-2��
ֱ��CD�Ľ���ʽ��y=-2x+8��
��y=0ʱ��-2x+8=0�����x=4��
��OC=4��
��2����ͼ1��
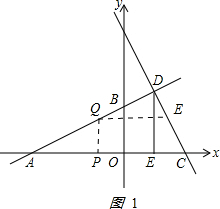 ��
��
�ٵ�-6��x��2ʱ����x=tʱ��y=
t+3��Q��t��
t+3����
QE��x�ᣬE����������
t+3��
��y=
t+3ʱ��
t+3=-2x+8�����x=-
t+
��
E��������ǣ�-
t+
��
t+3����
y=-
+
��
��ͼ2��
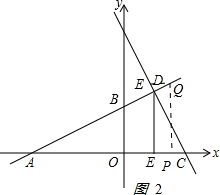
�ڵ�2��t��4ʱ����x=tʱ��y=
t+3��Q��t��
t+3����
QE��x�ᣬE����������
t+3��
��y=
t+3ʱ��
t+3=-2x+8��
���x=-
t+
��
E��������ǣ�-
t+
��
t+3����
y=t-��-
t+
��=
t-
��
������������-6��x��2ʱ��y=-
+
��
��2��t��4ʱ��y=
t-
��
��3����ͼ3��
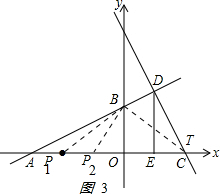
�ٵ�C��T���غ�ʱ����P1OB�ס�TOB����
=
�����P1O=4����P1��-4��0����
��P2OB�ס�BOT����
=
�����P2O=
����P2��-
��0����
��ͼ4��
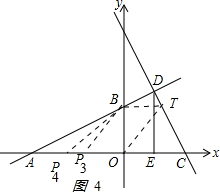
��y=3ʱ��3=-
x+8�����x=
����BT=
��
��T��C���غ�ʱ��BT��OB����TBO=��P3OB=90�㣬
��P3OB�ס�TBO����
=
��
���P3O=
��P3��-
��0����
��P4OB�ס�OBT����
=
��P4O=
��P4��-
��0����
����������P��-
��0������-
��0������-4��0������-
��0����
��OB=3��
D��DE��x���ڵ�E��2��0������
D��������2��
��x=2ʱ��y=
| 1 |
| 2 |
ֱ��CD y=kx+8����D��2��4������
2k+8=4��
���k=-2��
ֱ��CD�Ľ���ʽ��y=-2x+8��
��y=0ʱ��-2x+8=0�����x=4��
��OC=4��
��2����ͼ1��
 ��
���ٵ�-6��x��2ʱ����x=tʱ��y=
| 1 |
| 2 |
| 1 |
| 2 |
QE��x�ᣬE����������
| 1 |
| 2 |
��y=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
E��������ǣ�-
| 5 |
| 4 |
| 5 |
| 2 |
| 1 |
| 2 |
y=-
| 9 |
| 4 |
| 5 |
| 2 |
��ͼ2��

�ڵ�2��t��4ʱ����x=tʱ��y=
| 1 |
| 2 |
| 1 |
| 2 |
QE��x�ᣬE����������
| 1 |
| 2 |
��y=
| 1 |
| 2 |
| 1 |
| 2 |
���x=-
| 5 |
| 4 |
| 5 |
| 2 |
E��������ǣ�-
| 5 |
| 4 |
| 5 |
| 2 |
| 1 |
| 2 |
y=t-��-
| 5 |
| 4 |
| 5 |
| 2 |
| 9 |
| 4 |
| 5 |
| 2 |
������������-6��x��2ʱ��y=-
| 9 |
| 4 |
| 5 |
| 2 |
��2��t��4ʱ��y=
| 9 |
| 4 |
| 5 |
| 2 |
��3����ͼ3��

�ٵ�C��T���غ�ʱ����P1OB�ס�TOB����
| P1O |
| TO |
| BO |
| BO |
��P2OB�ס�BOT����
| P2O |
| OB |
| OB |
| OT |
| 9 |
| 4 |
| 9 |
| 4 |
��ͼ4��

��y=3ʱ��3=-
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
��T��C���غ�ʱ��BT��OB����TBO=��P3OB=90�㣬
��P3OB�ס�TBO����
| P3O |
| BT |
| BO |
| OB |
���P3O=
| 5 |
| 2 |
| 5 |
| 2 |
��P4OB�ס�OBT����
| P4O |
| OB |
| OB |
| TB |
| 18 |
| 5 |
| 18 |
| 5 |
����������P��-
| 5 |
| 2 |
| 18 |
| 5 |
| 9 |
| 4 |
���������⿼����һ�κ������ۺ��⣬�����˺���ֵ���Ա����Ĺ�ϵ�����������ε����ʣ����������ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
�ڡ�ABC�У���AB=AC����sinB���ڣ�������
A��sin
| ||
B��cos
| ||
| C��sinA | ||
| D��cosA |
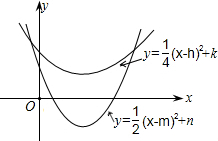 ͼ������ͬ�Գ�������������ߣ����й�ϵ����ȷ���ǣ�������
ͼ������ͬ�Գ�������������ߣ����й�ϵ����ȷ���ǣ�������| A��h=m | B��k��n |
| C��k=n | D��h��0��k��0 |
�����x+m����x-n���в���x��һ�����m��n���㣨������
| A��m=n | B��m=0 |
| C��m=-n | D��n=0 |
����ʽam+n�£�������=am-2�У������ڵĴ���ʽӦ�ǣ�������
| A��am+n-2 |
| B��an-2 |
| C��am+n+3 |
| D��an+2 |
��֪���ε��ܳ�Ϊ40cm��һ���Խ��߳�Ϊ16cm����������ε����Ϊ��������cm2��
| A��108 | B��114 |
| C��64 | D��96 |
 ��ͼ��ԲO�İ뾶Ϊ5��PA��PB��ԲO�����ߣ��е�ֱ�ΪA��B����APB=90�㣬��PA=
��ͼ��ԲO�İ뾶Ϊ5��PA��PB��ԲO�����ߣ��е�ֱ�ΪA��B����APB=90�㣬��PA=