题目内容
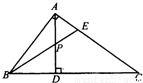
AD为Rt△ABC的斜边BC上的高,P是AD的中点,连BP并延长交AC于E.已知AC:AB=k.求AE:EC.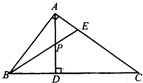
 解:过点A作BC的平行线交BE延长线于点F.
解:过点A作BC的平行线交BE延长线于点F.设BD=1,有AD=k,DC=k2.
∵AF∥BC,AD⊥BC,BA⊥AC
∴
 =
=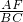 =
= =
= =
= =
= .
.分析:首先作出辅助线,利用相似三角形的性质,得出
 =
=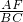 =
= ,再利用射影定理得出
,再利用射影定理得出 =
= ,从而求出答案.
,从而求出答案.点评:此题主要考查了相似三角形的性质,以及射影定理的有关性质,正确作出辅助线是解决问题的关键,作平行线是今后学习中常用辅助线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
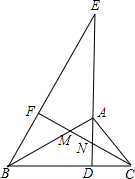 已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
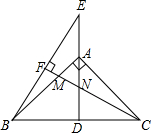 如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.