题目内容
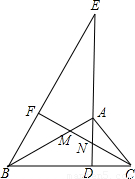
 如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.(1)若线段AM、AN的长是关于x的一元二次方程x2-2mx+n2-mn+
| 5 |
| 4 |
(2)若AN=
| 15 |
| 8 |
| 9 |
| 8 |
分析:(1)证明判别式△=0即可;
(2)充分利用题中的垂直关系,寻找已知和未知之间的关系,易证△EBD∽△CND,得DE:DC=BD:DN,即BD•DC=DN•ED.
因为AD⊥BC,则由射影定理有AD2=BD•DC,所以DN•ED=AD2.DN已知,AD易求,问题得解.
(2)充分利用题中的垂直关系,寻找已知和未知之间的关系,易证△EBD∽△CND,得DE:DC=BD:DN,即BD•DC=DN•ED.
因为AD⊥BC,则由射影定理有AD2=BD•DC,所以DN•ED=AD2.DN已知,AD易求,问题得解.
解答:解:(1)证明:△=(-2m)2-4(n2-mn+
m2)=-(m-2n)2≥0
∴(m-2n)2≤0
∴m-2n=0
∴△=0
∴一元二次方程x2-2mx+n2-mn+
m2=0
有两个相等的实数根
∴AM=AN;
(2)∵∠BAC=90°,AD⊥BC
∴∠ADC=∠ADB=90°,∠DAC=∠DBA
∴△ADC∽△BDA
∴
=
∴AD2=BD•DC
∵CF⊥BE
∴∠FCB+∠EBD=90°
∵∠E+∠EBD=90°
∴∠E=∠FCB
∵∠NDC=∠EDB=90°
∴△EBD∽△CND
∴
=
∴BD•DC=DN•ED
∴AD2=DN•ED
∵AN=
,DN=
∴AD=DN+AN=3
∴32=
DE
∴DE=8.
| 5 |
| 4 |
∴(m-2n)2≤0
∴m-2n=0
∴△=0
∴一元二次方程x2-2mx+n2-mn+
| 5 |
| 4 |
有两个相等的实数根
∴AM=AN;
(2)∵∠BAC=90°,AD⊥BC
∴∠ADC=∠ADB=90°,∠DAC=∠DBA
∴△ADC∽△BDA
∴
| AD |
| BD |
| DC |
| AD |
∴AD2=BD•DC
∵CF⊥BE
∴∠FCB+∠EBD=90°
∵∠E+∠EBD=90°
∴∠E=∠FCB
∵∠NDC=∠EDB=90°
∴△EBD∽△CND
∴
| ED |
| CD |
| BD |
| DN |
∴BD•DC=DN•ED
∴AD2=DN•ED
∵AN=
| 15 |
| 8 |
| 9 |
| 8 |
∴AD=DN+AN=3
∴32=
| 9 |
| 8 |
∴DE=8.
点评:此题考查了一元二次方程根的判别式与几何知识的结合、相似三角形的判定和性质,综合性强,难度较大.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
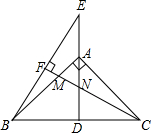
 已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点. 如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点. 的两个实数根,求证:AM=AN;
的两个实数根,求证:AM=AN; ,DN=
,DN= ,求DE的长.
,求DE的长. m2=0的两个实数根,求证:AM=AN;
m2=0的两个实数根,求证:AM=AN; ,DN=
,DN= ,求DE的长;
,求DE的长;
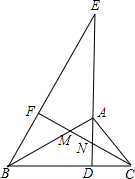
 m2=0的两个实数根,求证:AM=AN;
m2=0的两个实数根,求证:AM=AN;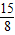 ,DN=
,DN= ,求DE的长;
,求DE的长;