题目内容
(1)如图(1),已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等(尺规作图,不写作法,保留作图痕迹,写出结论);
(2)如图(2),
(a)分别作出点P关于OA、OB的对称点P1、P2,连接P1P2,分别交OA、OB于点M、N
(b)若P1P2=5cm,则△PMN的周长为 .

(2)如图(2),
(a)分别作出点P关于OA、OB的对称点P1、P2,连接P1P2,分别交OA、OB于点M、N
(b)若P1P2=5cm,则△PMN的周长为

考点:作图-轴对称变换,角平分线的性质
专题:作图题
分析:(1)根据线段垂直平分线上的点到两端点的距离相等可得点P在CD的垂直平分线上,角平分线上的点到角的两边距离相等可得点P在∠AOB的平分线上,然后作线段CD的垂直平分线和∠AOB的平分线交点即为所求的点;
(2)(a)根据轴对称点的作法作出即可;
(b)根据轴对称的性质可得PM=P1M,PN=P2N,然后求出△PMN的周长=P1P2.
(2)(a)根据轴对称点的作法作出即可;
(b)根据轴对称的性质可得PM=P1M,PN=P2N,然后求出△PMN的周长=P1P2.
解答: 解:(1)如图所示,点P即为所求作的点;
解:(1)如图所示,点P即为所求作的点;
(2)(a)如图所示:
(b)∵点P关于OA、OB的对称点P1、P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2,
∵P1P2=5cm,
∴△PMN的周长=5cm.
故答案为:5cm.
 解:(1)如图所示,点P即为所求作的点;
解:(1)如图所示,点P即为所求作的点;(2)(a)如图所示:
(b)∵点P关于OA、OB的对称点P1、P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2,
∵P1P2=5cm,
∴△PMN的周长=5cm.
故答案为:5cm.
点评:本题考查了利用轴对称变换作图,轴对称的性质,线段垂直平分线上的点到两端点的距离相等的性质,角平分线上的点到角的两边距离相等的性质,熟记各性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 二次函数y=ax2+bx+c的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,求k的取值范围.
二次函数y=ax2+bx+c的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,求k的取值范围. 如图,AD、BC交于点O,P为AB、CD延长线的交点,且PA•PB=PC•PD.试说明:△PAD∽△PCB.
如图,AD、BC交于点O,P为AB、CD延长线的交点,且PA•PB=PC•PD.试说明:△PAD∽△PCB. 已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.
已知,如图,AB=AC,BD平分∠ABC,CD平分∠ACB.求证:AD⊥BC.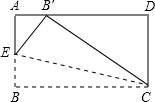 如图,一块矩形纸片的宽CD为2cm,点E在AB上,如果沿图中的EC对折,B点刚好落在AD上,此时∠BCE=15°,则BC的长为
如图,一块矩形纸片的宽CD为2cm,点E在AB上,如果沿图中的EC对折,B点刚好落在AD上,此时∠BCE=15°,则BC的长为 如图,圆内接四边形ABCD中,AC、BD相交于E,且AE=CE,求证:
如图,圆内接四边形ABCD中,AC、BD相交于E,且AE=CE,求证: