题目内容
 如图,AB为⊙O的直径,点D是
如图,AB为⊙O的直径,点D是 |
| AC |
(1)求证:△DAE∽△DBA;
(2)若DE=2,EB=4,求AD及AE的长.
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)如图,证明∠DAE=∠B,结合∠D=∠D,即可解决问题.
(2)由△DAE∽△DBA,列出比例式
=
,结合已知条件求出AD;运用勾股定理求出AE.
(2)由△DAE∽△DBA,列出比例式
| DE |
| AD |
| AD |
| BD |
解答: (1)证明:∵点D是
(1)证明:∵点D是
的中点,
∴
=
,
∴∠DAE=∠B,而∠D=∠D,
∴△DAE∽△DBA.
(2)解:∵△DAE∽△DBA,
∴
=
,
∵DE=2,BE=4,BD=6
∴AD=2
;
∵AB为⊙O的直径,
∴∠D=90°,
由勾股定理得:AE2=AD2+DE2,
∴AE=4.
即AD及AE的长分别为2
、4.
 (1)证明:∵点D是
(1)证明:∵点D是 |
| AC |
∴
 |
| AD |
 |
| DC |
∴∠DAE=∠B,而∠D=∠D,
∴△DAE∽△DBA.
(2)解:∵△DAE∽△DBA,
∴
| DE |
| AD |
| AD |
| BD |
∵DE=2,BE=4,BD=6
∴AD=2
| 3 |
∵AB为⊙O的直径,
∴∠D=90°,
由勾股定理得:AE2=AD2+DE2,
∴AE=4.
即AD及AE的长分别为2
| 3 |
点评:该题主要考查了圆周角定理及其推论、相似三角形的判定及其性质、勾股定理等几何知识点及其应用问题;牢固掌握圆周角定理及其推论、相似三角形的判定及其性质是解题的关键.

练习册系列答案
相关题目
 如图,已知AC∥BD,OA=OC,则下列结论不成立的是( )
如图,已知AC∥BD,OA=OC,则下列结论不成立的是( )| A、∠B=∠C |
| B、∠A=∠D |
| C、∠AOC=∠BOD |
| D、OA=OB |
 如图,在△ABC中,DE∥BC,AD=1,DB=2,DE=2,则BC=( )
如图,在△ABC中,DE∥BC,AD=1,DB=2,DE=2,则BC=( )| A、2 | B、4 | C、6 | D、8 |
 如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂红色对面是( )
如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂红色对面是( )| A、黄色 | B、黑色 | C、蓝色 | D、绿色 |
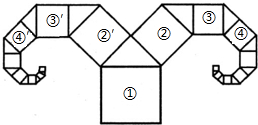 如图所示是一种“羊头”形图案,其作法是:从正方形①开始,以它的一条边为斜边作等腰直角三角形,然后再以这个等腰直角三角形两直角边为边作正方形②和②′,如此继续下去…,若正方形①的面积为a,则正方形⑦的边长是多少?正方形
如图所示是一种“羊头”形图案,其作法是:从正方形①开始,以它的一条边为斜边作等腰直角三角形,然后再以这个等腰直角三角形两直角边为边作正方形②和②′,如此继续下去…,若正方形①的面积为a,则正方形⑦的边长是多少?正方形 的边长是多少?
的边长是多少? 如图,⊙O是直径为4cm的圆形铁片,现用它截取最大的正方形ABCD.
如图,⊙O是直径为4cm的圆形铁片,现用它截取最大的正方形ABCD.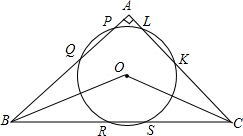 如图,在△ABC中,∠A为直角,⊙O与三角形三边交于点P、Q、R、S、K、L,若PQ=RS=KL,求∠BOC的大小.
如图,在△ABC中,∠A为直角,⊙O与三角形三边交于点P、Q、R、S、K、L,若PQ=RS=KL,求∠BOC的大小.