题目内容
15.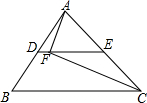 如图,在△ABC中,D、E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,若∠AFC=90°,EF=3DF,则BC的长为( )
如图,在△ABC中,D、E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,若∠AFC=90°,EF=3DF,则BC的长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
分析 根据直角三角形的性质得到EF=6,根据EF=3DF,得到DF=2,求出DE,根据三角形中位线定理解答即可.
解答 解:∵∠AFC=90°,点E是AC的中点,
∴EF=$\frac{1}{2}$AC=6,
∵EF=3DF,
∴DF=2,
∴DE=DF+EF=8,
∵D、E分别是AB,AC的中点,
∴BC=2DE=16,
故选:D.
点评 本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
6.到三角形三个顶点距离相等的点是( )
| A. | 三条边的垂直平分线的交点 | B. | 三条高线的交点 | ||
| C. | 三条边的中线的交点 | D. | 三条角平分线的交点 |
3.tan60°=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
20.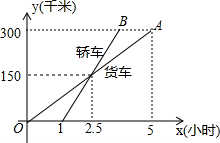 如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
 如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )
如图,在我省某高速公路上,一辆轿车和一辆货车沿相同的路线从M地到N地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,轿车比货车早到( )| A. | 1小时 | B. | 2小时 | C. | 3小时 | D. | 4小时 |
7.如果一次函数y=kx+2k+2的图象经过第一、二、三象限,则k的取值范围是( )
| A. | k>0 | B. | k$>-\frac{1}{2}$ | C. | k<0 | D. | -$\frac{1}{2}$<k<0 |
4.己知圆锥的底面半径为2cm,母线长为3cm,则该圆锥的侧面展开图的圆心角为( )
| A. | 60° | B. | 120° | C. | 90° | D. | 240° |
5.在以下实数:-$\sqrt{2}$,$\sqrt{16}$,π,3.1411,8,0.020020002…中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 如图是由5个大小相同的正方体摆成的立方体图形,它的主视图是图中的( )
如图是由5个大小相同的正方体摆成的立方体图形,它的主视图是图中的( )


