题目内容
 如图,在△ABC中,∠A=80°,且⊙O在三边上截得的弦长相等,则∠BOC的度数为
如图,在△ABC中,∠A=80°,且⊙O在三边上截得的弦长相等,则∠BOC的度数为考点:垂径定理,角平分线的性质,勾股定理
专题:
分析:先利用⊙O截△ABC的三条边所得的弦长相等,得出O是△ABC的内心,从而∠OBC=∠ABO,∠BCO=∠ACO,进一步求出∠BOC的度数.
解答:解:∵△ABC中∠A=70°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠OBC=∠ABO,∠BCO=∠ACO,
∵∠A=80°,
∴∠OBC+∠BCO=
(180°-∠A)=
(180°-80°)=50°,
∴∠BOC=180°-(∠OBC+∠BCO)=180°-50°=130°.
故答案为:130°.
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠OBC=∠ABO,∠BCO=∠ACO,
∵∠A=80°,
∴∠OBC+∠BCO=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠BCO)=180°-50°=130°.
故答案为:130°.
点评:本题考查的是垂径定理及三角形的内心,熟知三角形内心的性质是解答此题的关键.

练习册系列答案
相关题目
 将△BDE旋转一定的角度后得到△ADC,如图所示,如果BD=4cm,CD=2cm.
将△BDE旋转一定的角度后得到△ADC,如图所示,如果BD=4cm,CD=2cm. 如图是与“杨辉三角”有类似性质的数字三角形表,你能按照发现的规律把这个三角形继续写下去吗?和小伙伴比一比,看谁写得多.试试看.
如图是与“杨辉三角”有类似性质的数字三角形表,你能按照发现的规律把这个三角形继续写下去吗?和小伙伴比一比,看谁写得多.试试看.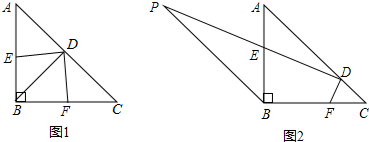
 如图,双曲线y=
如图,双曲线y=