题目内容
观察下列各式:
=
=
-
,
=
=
-
,
=
=
-
,
=
=
-
.
(1)请思考:
= ,
= ;
(2)你能发现上面各式的规律吗?请描述出来.
(3)设n为正整数,请你用含有字母n的等式表示上面的规律.
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 20 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
(1)请思考:
| 1 |
| 42 |
| 1 |
| 72 |
(2)你能发现上面各式的规律吗?请描述出来.
(3)设n为正整数,请你用含有字母n的等式表示上面的规律.
考点:规律型:数字的变化类
专题:
分析:分子是1,分母可以拆成两个连续自然数的乘积,就等于以这两个自然数为分母,分子为1的两个分数的差,由此规律解决问题即可.
解答:解:(1)
=
=
-
,
=
=
-
;
(2)分子是1,分母可以拆成两个连续自然数的乘积,就等于以这两个自然数为分母,分子为1的两个分数的差;
(3)
=
-
.
| 1 |
| 42 |
| 1 |
| 6×7 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 72 |
| 1 |
| 8×9 |
| 1 |
| 8 |
| 1 |
| 9 |
(2)分子是1,分母可以拆成两个连续自然数的乘积,就等于以这两个自然数为分母,分子为1的两个分数的差;
(3)
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
点评:此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
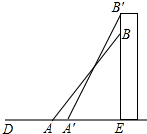 一根竹竿长a米,先像AB靠墙放置,与水平夹角为45°,为了减少占地空间,现将竹竿像A′B′放置,与水平夹角为60°,则竹竿让出多少水平空间( )
一根竹竿长a米,先像AB靠墙放置,与水平夹角为45°,为了减少占地空间,现将竹竿像A′B′放置,与水平夹角为60°,则竹竿让出多少水平空间( )A、(
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、(
|
若a,b互为相反数,c,d互为倒数,|m|=2,则代数式m2-3cd+
的值为( )
| a+b |
| m |
| A、-1 | B、1 | C、-2 | D、1或-7 |
半径是
,圆心角为36°的扇形的面积是( )
| 10 |
| A、π | ||||
B、
| ||||
C、
| ||||
| D、10π |
 操作探究:
操作探究: 如图,在△ABC中,∠A=80°,且⊙O在三边上截得的弦长相等,则∠BOC的度数为
如图,在△ABC中,∠A=80°,且⊙O在三边上截得的弦长相等,则∠BOC的度数为