题目内容
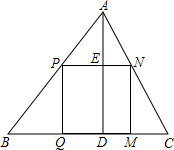
 如图,△ABC是一块锐角三角形材料,边BC=6cm,高AD=4cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,要使矩形EGFH的面积最大,EG的长应为 cm.
如图,△ABC是一块锐角三角形材料,边BC=6cm,高AD=4cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,要使矩形EGFH的面积最大,EG的长应为 cm.
【答案】分析:此题为二次函数的应用类试题,设EG=xcm,先根据相似求出EF,然后根据矩形面积公式求出S与x之间的解析式,运用公式求抛物线顶点的横坐标即可.
解答:解:设EG=xcm,由题意得△AEF∽△ABC,
∴ =
= ,
,
∴ ,
,
解得EF= .
.
∴S矩形EFHG=EG•EF= x.
x.
即S=- x2+6x.
x2+6x.
∴当x= =2时,矩形EGHF的面积最大.
=2时,矩形EGHF的面积最大.
点评:本题由相似三角形的实际问题,矩形EGHF的面积的表达,把问题转化为二次函数;利用二次函数的性质解决题目的问题.具有一定的综合性.
解答:解:设EG=xcm,由题意得△AEF∽△ABC,
∴
 =
= ,
,∴
 ,
,解得EF=
 .
.∴S矩形EFHG=EG•EF=
 x.
x.即S=-
 x2+6x.
x2+6x.∴当x=
 =2时,矩形EGHF的面积最大.
=2时,矩形EGHF的面积最大.点评:本题由相似三角形的实际问题,矩形EGHF的面积的表达,把问题转化为二次函数;利用二次函数的性质解决题目的问题.具有一定的综合性.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形一边在BC上,其余两个顶点分别在AB,AC上,那么这个正方形零件的边长应是
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形一边在BC上,其余两个顶点分别在AB,AC上,那么这个正方形零件的边长应是 19、如图:△ABC是一块直角三角形余料,∠C=90度,工人师傅把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请你协助工人师傅用尺规画出裁割线.(不写画法,保留作图痕迹)
19、如图:△ABC是一块直角三角形余料,∠C=90度,工人师傅把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上,请你协助工人师傅用尺规画出裁割线.(不写画法,保留作图痕迹) 如图,△ABC是一块锐角三角形材料,边BC=6cm,高AD=4cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,要使矩形EGFH的面积最大,EG的长应为
如图,△ABC是一块锐角三角形材料,边BC=6cm,高AD=4cm,要把它加工成一个矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,要使矩形EGFH的面积最大,EG的长应为 19、如图,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上.
19、如图,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使C为正方形的一个顶点,其余三个顶点分别在AB、BC、AC边上. 如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,则四边形DEFG最大面积为( )cm2.
如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,则四边形DEFG最大面积为( )cm2.