题目内容
7. 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求DE的长.
(3)在(2)的条件下,求AG的长.
分析 (1)首先连接OD,由DE为⊙O的切线,OC=OD,易得∠2+∠C=90°,又由OC⊥OB,可得∠C+∠OFC=90°,继而证得∠1=∠2;
(2)由OF:OB=1:3,⊙O的半径为3,可求得OF=1,然后由勾股定理得方程:32+x2=(x+1)2,继而求得答案;
(3)易证得Rt△EOD∽Rt△EGA,然后由相似三角形的对应边成比例,求得答案.
解答 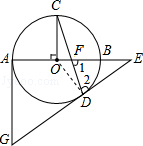 (1)证明:连结OD,
(1)证明:连结OD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,即∠2+∠ODC=90°,
∵OC=OD,
∴∠C=∠ODC,
∴∠2+∠C=90°,
∵OC⊥OB,
∴∠C+∠OFC=90°,
∴∠2=∠OFC,
∵∠1=∠OFC,
∴∠1=∠2;
(2)解:∵OF:OB=1:3,⊙O的半径为3,
∴OF=1,
∵∠1=∠2,
∴EF=ED,
在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,
∵OD2+DE2=OE2,
∴32+x2=(x+1)2,
解得x=4,
∴DE=4;
(3)解:∵AG为⊙O的切线,
∴AG⊥AE,
∴∠GAE=90°,
∴∠GAE=∠ODE=90°,
∵∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴$\frac{OD}{AG}$=$\frac{DE}{AE}$,
∵OE=4+1=5,
即$\frac{3}{AG}$=$\frac{4}{3+5}$,
∴AG=6.
点评 此题考查了切线的性质、勾股定理以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键,注意掌握方程思想的应用.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
2.下列说法正确的是( )
| A. | “打开电视机,正在播世界杯足球赛”是必然事件 | |
| B. | “掷一枚硬币正面朝上的概率是$\frac{1}{2}$”表示每抛掷硬币2次就有1次正面朝上 | |
| C. | 一组数据2,3,4,5,5,6的众数和中位数都是5 | |
| D. | 甲组数据的方差S甲2=0.09,乙组数据的方差S乙2=0.56,则甲组数据比乙组数据稳定 |
16.满足等式:(-2)3•(-2)x=-$\frac{1}{32}$的x的值为( )
| A. | -8 | B. | -5 | C. | 5 | D. | 3 |