题目内容
10. 如图,△ABC是等边三角形,P是∠ABC平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q,若BQ=2,则PE的长是2.
如图,△ABC是等边三角形,P是∠ABC平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q,若BQ=2,则PE的长是2.
分析 先根据△ABC是等边三角形,BP是∠ABC的平分线,可知∠EBP=30°,由PE⊥AB于点E,进而可得PE=$\frac{1}{2}$BP,然后由线段BP的垂直平分线交BC于点F,可得BP=2BQ=4,进而可求PE的长.
解答 解:∵△ABC是等边三角形,BP是∠ABC的平分线,
∴∠EBP=30°,
∵PE⊥AB于点E,
∴∠BEP=90°,
∴PE=$\frac{1}{2}$,
∵QF为线段BP的垂直平分线,
∴BP=2BQ,
∵BQ=2,
∴BP=4,
∴PE=2.
点评 本题考查的是等边三角形的性质、角平分线的性质及直角三角形的性质,熟知等边三角形的三个内角都是60°是解答此题的关键.

练习册系列答案
相关题目
18.2015年诺贝尔生理学或医学奖得主中国科学家屠呦呦,发现了一种病毒的长度约为0.00000456毫米,则数据0.00000456用科学记数法表示为( )
| A. | 0.456×10-5 | B. | 4.56×10-6 | C. | 4.56×10-7 | D. | 45.6×10-7 |
20.不等式2x+3≤5的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
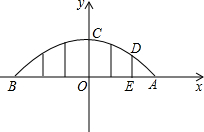 抛物线关于y轴对称,顶点C坐标为(0,9),交x轴于点A(d,0),B(-d,0)(d>0),如图将ABC视为抛物线形拱桥,五根拉杆均垂直于x轴,垂足依次在线段AB的6等分点上,h=9m,求拉杆DE的长度.
抛物线关于y轴对称,顶点C坐标为(0,9),交x轴于点A(d,0),B(-d,0)(d>0),如图将ABC视为抛物线形拱桥,五根拉杆均垂直于x轴,垂足依次在线段AB的6等分点上,h=9m,求拉杆DE的长度. 如图,抛物线y=x2+bx经过原点O,与x轴相交于点A(1,0),
如图,抛物线y=x2+bx经过原点O,与x轴相交于点A(1,0),