题目内容
20.解方程:(1)$\frac{x}{x-2}$-1=$\frac{8}{{x}^{2}-4}$.
(2)$\frac{x}{2x-1}$+$\frac{5}{1-2x}$=2.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x2+2x-x2+4=8,
解得:x=2,
经检验x=2是增根,分式方程无解;
(2)去分母得:x-5=4x-2,
解得:x=-1,
经检验x=-1是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
10.若分式$\frac{x+1}{{{x^2}+6}}$的值是为正数,则x的取值范围为( )
| A. | x>-1 | B. | x=-1 | C. | x≥-1 | D. | x<-1 |
5.甲、乙两名学生的十次数学竞赛训练成绩的平均分分别是115和116,成绩的方差分别是8.5和60.5,现在要从两人中选择发挥稳定的一人参加数学竞赛,下列说法正确的是( )
| A. | 甲、乙两人平均分相当,选谁都可以 | |
| B. | 乙的平均分比甲高,选乙 | |
| C. | 乙的平均分和方差都比甲高,成绩比甲稳定,选乙 | |
| D. | 两人的平均分相当,甲的方差小,成绩比乙稳定,选甲 |
12.下列判断错误的是( )
| A. | $\frac{2}{3}$是$\frac{4}{9}$的一个平方根 | B. | $\sqrt{2}$是$\sqrt{4}$的算术平方根 | ||
| C. | 平方根等于本身的数有0和1 | D. | (-4)2的算术平方根是4 |
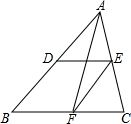 如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.
如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.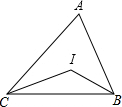 如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算:
如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算: