题目内容
5．
如图，圆锥的底面半径为6cm，高为8cm，求这个圆锥的侧面积和表面积．
分析 应先利用勾股定理求得圆锥的母线长，圆锥的侧面积=π×底面半径×母线长，把相关数值代入即可求解；
圆锥的表面积=圆锥的侧面积+圆锥的底面积=圆锥的侧面积+π×底面半径2，把相关数值代入即可求解．
解答 解：∵圆锥的底面半径为6cm，高为8cm，
∴圆锥的母线长为10cm，
∴S侧=π×6×10=60πcm2；
∵圆锥的底面积=π×62=36π，
∴S表=60π+36π=96πcm2．
点评 此题考查圆锥的侧面积和全面积的计算公式；用到的知识点为：圆锥的底面半径，高，母线长组成以母线长为斜边的直角三角形．
练习册系列答案
相关题目
13．
如图所示，在⊙O中，OB⊥OC于点O，则∠BAC的度数为（ ）
如图所示，在⊙O中，OB⊥OC于点O，则∠BAC的度数为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
20．将直角三角形的各边都缩小或扩大同样的倍数后，得到的三角形（ ）
| A． | 可能是锐角三角形 | B． | 不可能是直角三角形 | ||
| C． | 仍然是直角三角形 | D． | 可能是钝角三角形 |
如图，若△ADE∽△ACB，AB=8，AE=4，DE=3，则BC=6．
17．
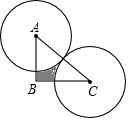如图，在Rt△ABC中，∠ABC=90°，AB=6cm，BC=8cm，分别以$\frac{1}{2}$AC的长为半径作圆，将Rt△ABC截去两个扇形，则余下阴影部分的面积为（ ）cm2．
如图，在Rt△ABC中，∠ABC=90°，AB=6cm，BC=8cm，分别以$\frac{1}{2}$AC的长为半径作圆，将Rt△ABC截去两个扇形，则余下阴影部分的面积为（ ）cm2．| A． | $\frac{25}{4}$P | B． | 24-$\frac{5}{4}$P | C． | 24-$\frac{25}{6}$P | D． | 24-$\frac{25}{4}$P |
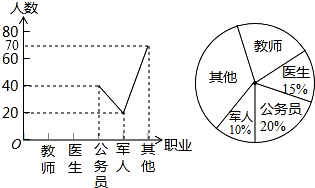某中学开展以“我最喜欢的职业”为主题的调查活动，通过对学生的随机抽样调查得到一组数据，并根据这组数据绘制下面两幅不完整的统计图：