题目内容
18.若点A(-2,a)和点B(4,b)在抛物线y=2(x-m)2上,且关于它的对称轴对称,则m=1.分析 由函数的解析式可知函数的对称轴为x=$\frac{-2+4}{2}$=m,从而得出m的值.
解答 解:由函数y=2(x-m)2可知这个函数的对称轴为x=m,
∵点A(-2,a)和点B(4,b)在抛物线y=2(x-m)2上,且关于它的对称轴对称,
∴对称轴x=$\frac{-2+4}{2}$=1,
∴m=1.
故答案为1.
点评 本题考查了二次函数图象上点的坐标特征,注意掌握二次函数图象上所经过的点,均能满足该函数的解析式.

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | $-\frac{1}{4}$xy3是整式 | B. | x3y2系数为0 | C. | $\frac{1}{a}$是单项式 | D. | 3不是单项式 |
6.已知a=|1-b|,b的相反数等于1.5,则a的值为( )
| A. | 2.5 | B. | 0.5 | C. | ±2.5 | D. | 1.5 |
3.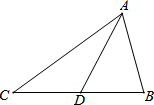 如图,△ABC中,点D在BC上,△ACD和△ABD面积相等,线段AD是三角形的( )
如图,△ABC中,点D在BC上,△ACD和△ABD面积相等,线段AD是三角形的( )
 如图,△ABC中,点D在BC上,△ACD和△ABD面积相等,线段AD是三角形的( )
如图,△ABC中,点D在BC上,△ACD和△ABD面积相等,线段AD是三角形的( )| A. | 高 | B. | 角平分线 | C. | 中线 | D. | 无法确定 |
8.等腰三角形的两边长分别为5cm,3cm,则该等腰三角形的周长为( )
| A. | 13cm | B. | 11cm | C. | 13cm或11cm | D. | 13cm或12cm |