题目内容
山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
| A型车 | B型车 | |
| 进货价格(元) | 1100 | 1400 |
| 销售价格(元) | 今年的销售价格 | 2000 |
考点:一次函数的应用,分式方程的应用,一元一次不等式的应用
专题:销售问题
分析:(1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由卖出的数量相同建立方程求出其解即可;
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由条件表示出y与a之间的关系式,由a的取值范围就可以求出y的最大值.
解答:解:(1)设今年A型车每辆售价x元,则去年售价每辆为(x+400)元,由题意,得
=
,
解得:x=1600.
经检验,x=1600是原方程的根.
答:今年A型车每辆售价1600元;
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由题意,得
y=(1600-1100)a+(2000-1400)(60-a),
y=-100a+36000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60-a≤2a,
∴a≥20.
∵y=-100a+36000.
∴k=-100<0,
∴y随a的增大而减小.
∴a=20时,y最大=34000元.
∴B型车的数量为:60-20=40辆.
∴当新进A型车20辆,B型车40辆时,这批车获利最大.
| 50000 |
| x+400 |
| 50000(1-20%) |
| x |
解得:x=1600.
经检验,x=1600是原方程的根.
答:今年A型车每辆售价1600元;
(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由题意,得
y=(1600-1100)a+(2000-1400)(60-a),
y=-100a+36000.
∵B型车的进货数量不超过A型车数量的两倍,
∴60-a≤2a,
∴a≥20.
∵y=-100a+36000.
∴k=-100<0,
∴y随a的增大而减小.
∴a=20时,y最大=34000元.
∴B型车的数量为:60-20=40辆.
∴当新进A型车20辆,B型车40辆时,这批车获利最大.
点评:本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,一次函数的解析式的运用,解答时由销售问题的数量关系求出一次函数的解析式是关键.

练习册系列答案
相关题目
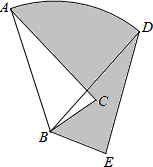 如图,在△ABC中,AB=6,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是( )
如图,在△ABC中,AB=6,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是( )| A、6π | B、5π | C、4π | D、3π |
 如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.
如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.

 如图,为估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA,OB的中点M,N,测得MN=32m,则A,B两点间的距离是
如图,为估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA,OB的中点M,N,测得MN=32m,则A,B两点间的距离是