题目内容
如图，在⊙O中，半径OC与弦AB垂直，垂足为E，以OC为直径的圆与弦AB的一个交点为F，D是CF延长线与⊙O的交点．若OE=4，OF=6，求⊙O的半径和CD的长．考点：垂径定理,勾股定理,圆周角定理,相似三角形的判定与性质
专题：计算题,几何图形问题
分析：由OE⊥AB得到∠OEF=90°，再根据圆周角定理由OC为小圆的直径得到∠OFC=90°，则可证明Rt△OEF∽Rt△OFC，然后利用相似比可计算出⊙O的半径OC=9；接着在Rt△OCF中，根据勾股定理可计算出CF=3
，由于OF⊥CD，根据垂径定理得CF=DF，所以CD=2CF=6
．
| 5 |
| 5 |
解答：解：∵OE⊥AB，
∴∠OEF=90°，
∵OC为小圆的直径，
∴∠OFC=90°，
而∠EOF=∠FOC，
∴Rt△OEF∽Rt△OFC，
∴OE：OF=OF：OC，即4：6=6：OC，
∴⊙O的半径OC=9；
在Rt△OCF中，OF=6，OC=9，
∴CF=
=3
，
∵OF⊥CD，
∴CF=DF，
∴CD=2CF=6
．
∴∠OEF=90°，
∵OC为小圆的直径，
∴∠OFC=90°，
而∠EOF=∠FOC，
∴Rt△OEF∽Rt△OFC，
∴OE：OF=OF：OC，即4：6=6：OC，
∴⊙O的半径OC=9；
在Rt△OCF中，OF=6，OC=9，
∴CF=
| OC2-OF2 |
| 5 |
∵OF⊥CD，
∴CF=DF，
∴CD=2CF=6
| 5 |
点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理、圆周角定理和相似三角形的判定与性质．
练习册系列答案
阅读快车系列答案
相关题目
若
有意义，则m的取值范围是（ ）
| m-3 |
| A、m＞3 | B、m≥3 |
| C、m＜3 | D、m≤3 |
如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．
在平面直角坐标系xOy中，已知抛物线y=x2-2mx+m2-9．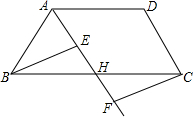
如图，在四边形ABCD中，点H是BC的中点，作射线AH，在线段AH及其延长线上分别取点E，F，连结BE，CF．