题目内容
若m、n(m<n)是关于x的方程1-(x-a)(x-b)=0的两根,且a<b,则a、b、m、n的大小关系是 .
考点:根与系数的关系,根的判别式
专题:数形结合
分析:方程变形为(x-a)(x-b)=1,利用二次函数与异次函数图象解决问题:二次函数y=(x-a)(x-b)与x轴两个交点坐标为(a,0),(b,0),且直线y=1与抛物线y=(x-a)(x-b)的交点的横坐标分别为m与n,于是可得到则a、b、m、n的大小关系.
解答:解:(x-a)(x-b)=1,
二次函数y=(x-a)(x-b)与x轴两个交点坐标为(a,0),(b,0),
则直线y=1与抛物线y=(x-a)(x-b)的交点的横坐标分别为m与n,
所以m<a<b<n.
故答案为m<a<b<n.
二次函数y=(x-a)(x-b)与x轴两个交点坐标为(a,0),(b,0),
则直线y=1与抛物线y=(x-a)(x-b)的交点的横坐标分别为m与n,
所以m<a<b<n.
故答案为m<a<b<n.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了图象法解决数学问题.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
将二次函数y=x2的图象向上平移m(m>0)个单位再向右平移2个单位,则平移以后的二次函数的解析式为( )
| A、y=(x+2)2-m |
| B、y=(x+2)2+m |
| C、y=(x+m)2+2 |
| D、y=(x-2)2+m |
已知a是锐角,若sina=
,则锐角a是( )
| ||
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
如图,在长为32m,宽为20m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( )
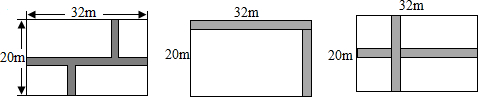

| A、32×20-32x-20x=540 |
| B、(32-x)(20-x)+x2=540 |
| C、(32-x) (20-x)=540 |
| D、32x+20x=540 |