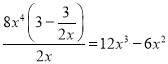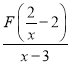题目内容
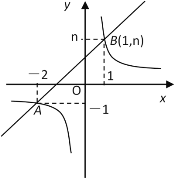
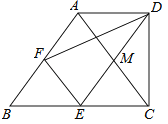
【题目】如图4，在梯形ABCD中，AD∥BC，∠BCD=90°，BC=2AD，F，E分别是AB，BC的中点，则下列结论不一定正确的是（ ）
A.△ABC是等腰三角形B.四边形EFAM是菱形
C.
D.DE平分∠CDF
【答案】D
【解析】
试题连接AE，如图所示，
∵E为BC的中点，
∴BE=CE=
BC，又BC=2AD，
∴AD=BE=EC，又AD∥BC，
∴四边形ABED为平行四边形，四边形AECD为平行四边形，
又∵∠DCB=90°，
∴四边形AECD为矩形，
∴∠AEC=90°，即AE⊥BC，
∴AE垂直平分BC，
∴AB=AC，即△ABC为等腰三角形，
故选项A不合题意；
∵E为BC的中点，F为AB的中点，
∴EF为△ABC的中位线，
∴EF∥AC，EF=AC，
又∵四边形ABED为平行四边形，
∴AF∥ME，
∴四边形AFEM为平行四边形，
又∵AF=AB=AC=EF，
∴四边形AFEM为菱形，
故选项B不合题意；
过F作FN⊥BC于N点，可得FN∥AE，
又∵F为AB的中点，
∴N为BE的中点，
∴FN为△ABE的中位线，
∴FN=AE，
又∵AE=DC，BE=AD，
∴S△BEF=S△ACD，
故选项C不合题意；
DE不一定平分∠CDF，
故选项D符合题意．
故选D．
练习册系列答案
相关题目
