Question

【题目】已知正方形，点是其内部一点.

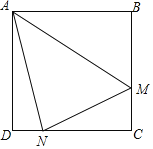
（1）如图1，点在边的垂直平分线上，将绕点逆时针旋转，得到，当点落在上时，恰好点落在直线上，求的度数；

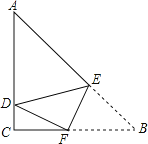
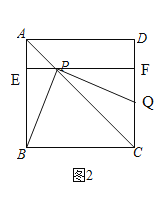
（2）如图2，点在对角线上，连接，若将线段绕点逆时针旋转后得到线段，试问点是否在直线上，请给出结论，并说明理由；

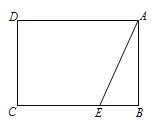
（3）如图3，若，设，，，请写出、、这三条线段长之间满足的数量关系是____________.

Answer 1

【答案】（1）；（2）点在直线上，理由见解析；（3）

【解析】

（1）根据中垂线的性质和旋转的性质判定是等边三角形，从而求解；

（2）根据题意证明∴，从而求证；

（3）把△ABP绕点A逆时针旋转90°，绕点B顺时针旋转90°，根据旋转变换只改变图形的位置不改变图形的形状可得等腰直角三角形，根据等腰直角三角形的性质和勾股定理得出结论，等量代换求解．

连接，

∵点在边的垂直平分线上，

∴.

又∵，

∴是等边三角形，

∴，

∴，

∴.

（2）点在直线上.证明如下：

作交于点，过点作交于点交于点.

∴，

∴，

∴

又∵在正方形对角线上，∴∠EAP=∠APE=45°

∴，

∵，

∴，

∴，

∴.

即将线段绕点8逆时针旋转后得到线段，点在直线上.

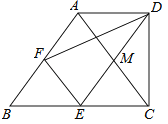
（3）

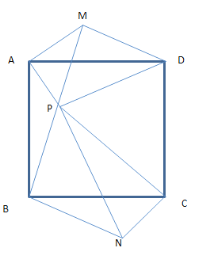
如图，将△ABP绕点A逆时针旋转90°得到△AMD，

由题意可知：∠APB=∠AAMD=135°，DM=BP,AP=AM=a，∠PAM=90°

∴∠AMP=45°

∴∠PMD=90°

∴在Rt△APM中，

在Rt△PMD中，

∴

将△ABP绕点B顺时针旋转90°得到△BNC，同理可证

在Rt△PNC中，

在Rt△BPN中，

∴

所以可得：

整理得：

.