题目内容
在△ABC中，以AB为直径的圆交BC于点D，交AC于点E，且 |
| BD |
|
| DE |
考点：圆周角定理,等腰三角形的判定,圆心角、弧、弦的关系
专题：证明题
分析：连接AD，根据AB是⊙O的直径可知∠ADB=90°，即ADF⊥BC，再由
=
得出∠BAD=∠CAD，故可得出结论．
|
| BD |
|
| DE |
解答：
解：连接AD，
∵AB是⊙O的直径，
∴∠ADB=90°，即AD⊥BC．
∵
=
，
∴∠BAD=∠CAD，
∴AB=AC，即△ABC是等腰三角形．
解：连接AD，∵AB是⊙O的直径，
∴∠ADB=90°，即AD⊥BC．
∵
|
| BD |
|
| DE |
∴∠BAD=∠CAD，
∴AB=AC，即△ABC是等腰三角形．
点评：本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
△ABC中，∠C=90°，⊙O是△ABC的内切圆．AB=8，⊙O的半径为2，则△ABC的周长是
已知AB⊥BF，DE⊥BF，垂足分别为点B、E，C为BF上的一点，且AB=DE，AC=DF，求证：BE=CF．下面是按一定规律排列的一列数：
第1个数：
-（1+
）；
第2个数：
-（1+
）（1+
）（1+
）；
第3个数：
-（1+
）（1+
）（1+
）（1+
）（1+
）；
…
第n个数：
-（1+
）（1+
）（1+
）…（1+
）．
那么，在第2011个数、第2012个数、第2013个数、第2014个数中，最大的数是（ ）
第1个数：
| 1 |
| 2 |
| -1 |
| 2 |
第2个数：
| 1 |
| 3 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
第3个数：
| 1 |
| 4 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)4 |
| 5 |
| (-1)5 |
| 6 |
…
第n个数：
| 1 |
| n+1 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)2n-1 |
| 2n |
那么，在第2011个数、第2012个数、第2013个数、第2014个数中，最大的数是（ ）
| A、第2011个数 |
| B、第2012个数 |
| C、第2013个数 |
| D、第2014个数 |
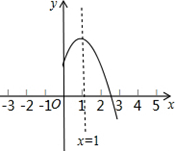二次函数y=ax2+bx+c（a≠0）的图象的对称轴是直线x=1，其图象的一部分如图所示则①abc＜0；②a-b+c＜0；③3a+c＜0；④当-1＜x＜3时，y＞0．其中判断正确的有（ ）个．