题目内容
10. 如图,已知△ABC中,∠ACB=120°,CF平分∠ACB,AD∥EC,交BC的延长线于点D,试判断△ACD是等腰三角形吗?请推理说明你的结论.
如图,已知△ABC中,∠ACB=120°,CF平分∠ACB,AD∥EC,交BC的延长线于点D,试判断△ACD是等腰三角形吗?请推理说明你的结论.
分析 根据题意即可推出∠D=60°,∠CAD=60°,然后根据三角形内角和定理,即可推出∠ACD=60°,即可推出△ACD是等腰三角形.
解答 解:是等腰三角形.
理由:∵∠ACB=120°,CF平分∠ACB,
∴∠BCF=60°,
∵AD∥FC,
∴∠BCF=∠D=∠CAD=60°,
∴∠ACD=60°,
∴△ACD是等边三角形,
即是等腰三角形.
点评 本题主要考查等边三角形的判定、平行性的性质、角平分线的性质、三角形内角和定理,关键在于推出∠BCF=∠D=∠CAD=60°.

练习册系列答案
相关题目
20.下列事件为必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | |
| B. | 打开电视机,正在播放动画片 | |
| C. | 两角及一边对应相等的两个三角形全等 | |
| D. | 三根长度为2cm、3cm、5cm的木棒首尾相接能摆成三角形 |
2.某市客运管理部门对“十一”国庆假期七天客流变化量进行了不完全统计,数据如下(用正数表示客流量比前一天上升数,用负数表示比前一天下降数).
与9月30日相比,10月7日的客流量是上升了还是下降了?变化了多少?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 变化/万人 | 20 | -3 | -10 | -3 | 2 | 9 | 3 |
19.已知a<b,则下列式子正确的是( )
| A. | a-3>b-3 | B. | a+1>b+1 | C. | 2a>2b | D. | -5a>-5b |
 如图,某幢大楼顶部有一块广告牌MN,某人用高为1.5米的测角仪分别在B、D两处测得点N和M的仰角∠NAE、∠MCE分别为45°和60°,若BD=8m,DF=15m,求楼高NF及广告牌高MN.(取$\sqrt{3}$≈1.73)
如图,某幢大楼顶部有一块广告牌MN,某人用高为1.5米的测角仪分别在B、D两处测得点N和M的仰角∠NAE、∠MCE分别为45°和60°,若BD=8m,DF=15m,求楼高NF及广告牌高MN.(取$\sqrt{3}$≈1.73)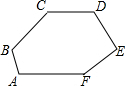 如图,已知在六边形ABCDEF中,CD∥AF,∠D=∠A,AB⊥BC,∠C=124°,∠E=80°,求∠F的度数.(提示:延长CB与FA的延长线交于点G)
如图,已知在六边形ABCDEF中,CD∥AF,∠D=∠A,AB⊥BC,∠C=124°,∠E=80°,求∠F的度数.(提示:延长CB与FA的延长线交于点G)