Question

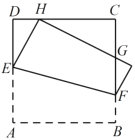
【题目】如图，将正方形折叠，使顶点与边上的一点重合（不与端点，重合），折痕交于点，交于点，边折叠后与边交于点，设正方形的周长为，的周长为，则的值为（ ）

A.B.C.D.2

Answer 1

【答案】D

【解析】

设正方形ABCD的边长为a，CH=x，DE=y，则m=4a，根据折叠的性质可得∠EHG=∠A=90°，EH=AE，可得EH=a-y，DH=a-x，根据直角三角形两锐角互余的关系可得∠DEH=∠CHG，可证明△DEH∽△CHG，根据相似三角形的性质可用a、x、y表示出CG、HG的长，在Rt△DEH中利用勾股定理可得x2=2a(x-y)，表示出△CHG的周长，进而可得答案．

设正方形ABCD的边长为a，CH=x，DE=y，则m=4a，

∵将正方形折叠，使顶点与边上的一点重合，

∴∠EHG=∠A=90°，EH=AE，

∴DH=a-x，EH=a-y，

∵∠CHG+∠DHE=90°，∠DEH+∠DHE=90°，

∴∠CHG=∠DEH，

∵∠D=∠C=90°，

∴△DEH∽△CHG，

∴，即：，

∴CG=，HG=，

在Rt△DEH中，EH2=DE2+DH2，即(a-y)2=y2+(a-x)2，

∴x2=2a(x-y)，

∴n=CH+HG+CG=x++==2a，

∴==2，

故选：D．