题目内容
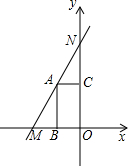 如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C.矩形ABOC的面积为2.
如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C.矩形ABOC的面积为2.(1)点M的坐标为
(2)求直线MN的解析式;
(3)求点A的坐标(结果用根号表示).
考点:待定系数法求一次函数解析式,解一元二次方程-公式法
专题:
分析:(1)由点N(0,6),得出ON=6,再由ON=3OM,求得OM=2,又吐得出点M的坐标;
(2)设出直线MN的解析式为:y=kx+b,代入M、N两点求得答案即可;
(3)设出点A坐标,表示出OB、AB的长,利用矩形的面积建立方程,求得答案即可.
(2)设出直线MN的解析式为:y=kx+b,代入M、N两点求得答案即可;
(3)设出点A坐标,表示出OB、AB的长,利用矩形的面积建立方程,求得答案即可.
解答:解:(1)M(-2,0);
(2)设直线MN的解析式为:y=kx+b,
分别把M(-2,0),N(0,6)坐标代入其中,得
,
解得
,
∴直线MN的解析式为:y=3x+6;
(3)设点A的坐标为(x,y).
∵点A在线段MN上,
∴y=3x+6,且-2<x<0.
根据题意,得OB•AB=2,
∵OB=-x,AB=y,
∴-x(3x+6)=2,
整理得:3x2+6x+2=0,
解得x=-1±
.
当x=-1+
时,y=3+
;
当x=-1-
时,y=3-
.
∴点A的坐标为A(-1+
,3+
)
或A(-1-
,3-
).
(2)设直线MN的解析式为:y=kx+b,
分别把M(-2,0),N(0,6)坐标代入其中,得
|
解得
|
∴直线MN的解析式为:y=3x+6;
(3)设点A的坐标为(x,y).
∵点A在线段MN上,
∴y=3x+6,且-2<x<0.
根据题意,得OB•AB=2,
∵OB=-x,AB=y,
∴-x(3x+6)=2,
整理得:3x2+6x+2=0,
解得x=-1±
| ||
| 3 |
当x=-1+
| ||
| 3 |
| 2 |
当x=-1-
| ||
| 3 |
| 2 |
∴点A的坐标为A(-1+
| ||
| 3 |
| 2 |
或A(-1-
| ||
| 3 |
| 2 |
点评:此题考查待定系数法求函数解析式,以及利用一次函数解决实际问题和矩形的面积的运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
下列运算中,正确的是( )
| A、x2+x2=x4 |
| B、x6÷x2=x3 |
| C、x2•x4=x6 |
| D、(3x2)2=6x4 |
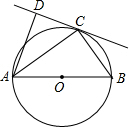 已知:AB为⊙O的直径,C为⊙O上一点,CD是⊙O的切线,AD⊥CD于D.
已知:AB为⊙O的直径,C为⊙O上一点,CD是⊙O的切线,AD⊥CD于D. 如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是
如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是