题目内容
老师给出一个函数,甲、乙、丙、丁四人各指出这个函数的一个性质,甲:函数图象不在第二象限;乙:函数图象与坐标轴无交点;丙:y随x的增大而减小;丁:当x=2时,y=30.已知这四人叙述都正确,请构造出满足上述所有性质的一个函数________.
y=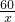 (答案不唯一).
(答案不唯一).
分析:根据此函数图象与坐标轴无交点可知此函数是反比例函数,设其解析式为y= (k≠0),根据函数图象不在第二象限,y随x的增大而减小可知k>0,由当x=2时,y=30即可求出k的值,进而得出结论.
(k≠0),根据函数图象不在第二象限,y随x的增大而减小可知k>0,由当x=2时,y=30即可求出k的值,进而得出结论.
解答:∵函数图象与坐标轴无交点,
∴此函数是反比例函数,
设其解析式为y= (k≠0),
(k≠0),
∵函数图象不在第二象限,y随x的增大而减小,由当x=2时,y=30,
∴30= ,解得k=60.
,解得k=60.
∴此函数的解析式为:y=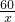 (答案不唯一).
(答案不唯一).
故答案为:y=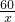 (答案不唯一).
(答案不唯一).
点评:本题考查的是反比例函数的性质,此题属开放性题目,答案不唯一,只要写出的答案符合条件即可.
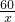 (答案不唯一).
(答案不唯一).分析:根据此函数图象与坐标轴无交点可知此函数是反比例函数,设其解析式为y=
 (k≠0),根据函数图象不在第二象限,y随x的增大而减小可知k>0,由当x=2时,y=30即可求出k的值,进而得出结论.
(k≠0),根据函数图象不在第二象限,y随x的增大而减小可知k>0,由当x=2时,y=30即可求出k的值,进而得出结论.解答:∵函数图象与坐标轴无交点,
∴此函数是反比例函数,
设其解析式为y=
 (k≠0),
(k≠0),∵函数图象不在第二象限,y随x的增大而减小,由当x=2时,y=30,
∴30=
 ,解得k=60.
,解得k=60.∴此函数的解析式为:y=
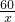 (答案不唯一).
(答案不唯一).故答案为:y=
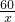 (答案不唯一).
(答案不唯一).点评:本题考查的是反比例函数的性质,此题属开放性题目,答案不唯一,只要写出的答案符合条件即可.

练习册系列答案
相关题目