题目内容
5.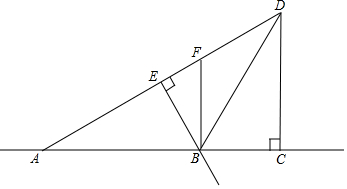 如图所示,DB是∠ADC的平分线,AC⊥CD,∠BED=90°,BF∥CD,∠ADB=30°.
如图所示,DB是∠ADC的平分线,AC⊥CD,∠BED=90°,BF∥CD,∠ADB=30°.请根据条件填空或解答:
(1)∠ACD=90°(注:填角的度数),直线AD与BE的位置关系是AD⊥BE;
(2)在线段DA、DB、DC中,最短的线段是DC.理由是垂线段最短.
(3)求∠FBD的度数(要求写出推理过程和推理的依据).
分析 (1)根据垂线的定义以及性质即可解决问题;
(2)根据垂线段最短即可解决问题;
(3)由BF∥CD,推出∠DBF=∠BDC,求出∠CDB即可解决问题;
解答 解:(1)∵AC⊥CD,
∴∠ACD=90°,
∵∠BED=90°,
∴BE⊥AD,
故答案为∠ACD=90°,AD⊥BE.
(2)在线段DA、DB、DC中,最短的线段是 DC.理由是垂线段最短.
故答案为CD,垂线段最短.
(3)∵BD平分∠ADC,∠ADB=30°,
∴∠CDB=∠ADB=30°,
∵BF∥CD,
∴∠DBF=∠BDC=30°,
点评 本题考查平行线的性质、垂线的定义和性质、垂线段最短等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.直角三角形的两个锐角平分线的夹角是( )
| A. | 45° | B. | 135° | ||
| C. | 45°或135° | D. | 由两个锐角的大小决定 |
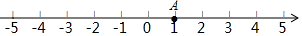 如图,在数轴上,点A表示的数是1,现将点A沿数轴做如下移动,第一次点A向左移动3 个单位长度到达点A1,点A1表示的数是-2;
如图,在数轴上,点A表示的数是1,现将点A沿数轴做如下移动,第一次点A向左移动3 个单位长度到达点A1,点A1表示的数是-2;