题目内容
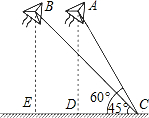（2013•工业园区模拟）在一个阳光明媚、清风徐徐的周末，小明和小强一起到郊外放风筝．他们把风筝放飞后，两个风筝的引线一端都固定在地面上的C处（如图）．现已知风筝A的引线（线段AC）长20m，风筝B的引线（线段BC）长24m，在C处测得风筝A的仰角为60°，风筝B的仰角为45°．（1）试通过计算，比较风筝A与风筝B谁离地面更高？
（2）求风筝A与风筝B的水平距离．（结果精确到0.01m，
| 2 |
| 3 |
分析：（1）在直角三角形中，运用三角函数定义求得线段BE和AD的长，比较后即可得到谁飞的更高；
（2）利用已知角的余弦函数求CE，CD．距离=CE-CD．
（2）利用已知角的余弦函数求CE，CD．距离=CE-CD．
解答：解；（1）分别过A、B作地面的垂线，垂足分别为D、E．
在Rt△ADC中，∵AC=20，∠ACD=60°，
∴AD=20×sin60°=10
≈17.32（m）．
在Rt△BEC中，∵BC=24，∠BCE=45°，
∴BE=24×sin45°=12
≈16.97（m）
∵17.32＞16.97，∴风筝A比风筝B离地面更高．
（2）在Rt△ADC中，
∵AC=20，∠ACD=60°，∴DC=20×cos60°=10（m）．
在Rt△BEC中，
∵BC=24，∠BCE=45°，∴EC=BE≈16.97（m）
∴EC-DC≈16.97-10=6.97（m）
即风筝A与风筝B的水平距离约为6.97 m．
在Rt△ADC中，∵AC=20，∠ACD=60°，
∴AD=20×sin60°=10
| 3 |
在Rt△BEC中，∵BC=24，∠BCE=45°，
∴BE=24×sin45°=12
| 2 |
∵17.32＞16.97，∴风筝A比风筝B离地面更高．
（2）在Rt△ADC中，
∵AC=20，∠ACD=60°，∴DC=20×cos60°=10（m）．
在Rt△BEC中，
∵BC=24，∠BCE=45°，∴EC=BE≈16.97（m）
∴EC-DC≈16.97-10=6.97（m）
即风筝A与风筝B的水平距离约为6.97 m．
点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形，解题的关键是从实际问题中抽象出直角三角形．
练习册系列答案
名校课堂系列答案
相关题目
（2013•工业园区二模）某班50名同学积极响应“为雅安地震灾区献爱心捐款活动”，并将所捐款情况统计并制成统计图，根据图中信息，捐款金额的众数和中位数分别是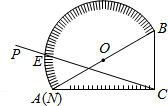
（2013•工业园区二模）如图，量角器的直径与直角三角板ABC的斜边AB重合，其中AB=8cm，量角器O刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转，CP与量角器的半圆弧交于点E，第35秒时，点E在量角器上对应划过的
（2013•工业园区二模）如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．当线段AM最短时，重叠部分的面积是