Question

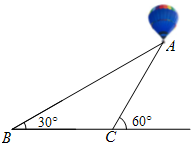如图，天空中有一个静止的热气球A，从地面点B测得A的仰角为30°，从地面点C测得A的仰角为60°．已知BC=50m，点A和直线BC在同一垂直平面上，求热气球离地面的高度．

Answer 1

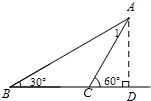解：过点A作AD⊥BC于点D，
∴∠ADC=90°，
∵∠B=30°，∠ACD=60°，
∴∠1=30°，
∴∠1=∠B，∴CA=CB=50m，
在Rt△ACD中，sin∠ACD=，
∴，
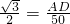∴AD=25m．
答：热气球离地面的高度是25米．
分析：过点A作AD⊥BC，交BC于点D；本题涉及到两个直角三角形△ADC、△ABD，应利用其公共边AD构造等量关系，解三角形可得AD与AC的关系；进而可求出答案．
点评：本题考查俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．