题目内容
2．若△ABC∽△DEF，且$\frac{AB}{DE}$=$\frac{1}{3}$，则$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=$\frac{1}{9}$．分析 根据相似三角形的面积的比等于相似比的平方进行计算．
解答 解：∵△ABC∽△DEF，
∴$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=（$\frac{AB}{DE}$）2=（$\frac{1}{3}$）2=$\frac{1}{9}$．
故答案为$\frac{1}{9}$．
点评 本题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等；相似三角形（多边形）的周长的比等于相似比；相似三角形的面积的比等于相似比的平方．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
13．某班开展跳绳比赛，5名同学的成绩如下（单位：个）：137，140，142，138，140，这组数据的中位数是（ ）
| A． | 137 | B． | 138 | C． | 140 | D． | 142 |
已知△ABC与△CDE都是等腰直角三角形，∠ACB=90°，∠DCE=90°，连结BE，AD，相交于点F．求证：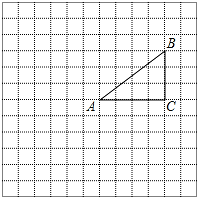
正方形网格中的每个小正方形的边长都是1，顶点叫做格点．△ABC的三个顶点A、B、C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△A′B′C′．
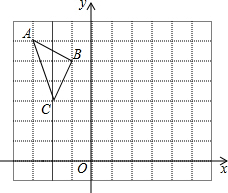如图，已知△ABC请画出△ABC关于y轴对称的图形△A′B′C′并按要求填空．（方格的边长为1）
实数a、b、c在数轴上的对应点如图所示，化简$|{b-a}|+\sqrt{{{（{b-c}）}^2}}-\sqrt{a^2}$．