题目内容
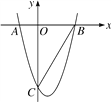
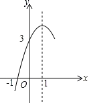
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴一个交点的坐标为(-1,0),其部分图象如图所示,下列结论:
轴一个交点的坐标为(-1,0),其部分图象如图所示,下列结论:
![]() ;
;![]() ;
;![]() 方程
方程![]() 的两个根是
的两个根是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .其中结论正确的是_____________(填写正确结论的标号)
.其中结论正确的是_____________(填写正确结论的标号)
【答案】①③④
【解析】
利用抛物线开口方向以及与y轴的交点情况可对①进行判断;根据对称轴的位置结合开口方向,则可对②进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为(3,0),则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断.
解:∵抛物线开口向下,
∴a<0,
∵抛物线与y轴交于点(0,3),
∴c=3>0,
∴ac<0,所以①正确;
∵抛物线的对称轴为直线x=1,
∴![]() =1,
=1,
∴b=2a>0,所以②错误;
∵抛物线的对称轴为直线x=1,
而点(1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=1,x2=3,所以③正确;
∴当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,所以④正确;
,所以④正确;
故答案为①③④.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .