Question

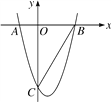
【题目】如图，已知抛物线y＝x2－x－6与x轴交于点A和B，点A在点B的左边，与y轴的交点为C.

(1)用配方法求该抛物线的顶点坐标；

(2)求sin∠OCB的值；

(3)若点P(m，m)在该抛物线上，求m的值．

Answer 1

【答案】(1)抛物线的顶点坐标为;(2) sin∠OCB＝;(3) m1＝1＋，m2＝1－.

【解析】（1）根据配方法，可得顶点式解析式，根据顶点式解析式，可得抛物线的顶点；

（2）根据函数值为0，可得B点坐标，根据自变量为0，可得C点坐标，根据勾股定理，可得BC的长，根据正弦的意义，可得答案；

（3）根据图象上的点的坐标满足函数解析式，可得一元二次方程，根据解一元二次方程，可得答案．

解：(1)∵y=x2x6=x2x+6=(x )2，

∴抛物线的顶点坐标为(,)；

(2)令x2x6=0,

解得x1=2,x2=3，

∴点B的坐标为(3,0),

又点C的坐标为(0,6)，

∴BC=，

∴sin∠OCB=；

(3)∵点P(m,m)在这个二次函数的图象上，

∴m2m6=m，

即m22m6=0，

解得m1＝1＋，m2＝1－.