ЬтФПФкШн
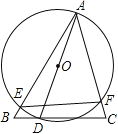
ЁОЬтФПЁПвбжЊЃКШчЭМ.дкЁїABCжа.AB=AC=5cmЃЌBC=6cm.ЕуPгЩBГіЗЂЃЌбиBCЗНЯђдШЫйдЫЖЏ.ЫйЖШЮЊ1cm/s.ЭЌЪБЃЌЕуQДгЕуAГіЗЂЃЌбиACЗНЯђдШЫйдЫЖЏ.ЫйЖШЮЊ1cm/sЃЌЙ§ЕуPзїPM![]() BCНЛABгкЕуMЃЌЙ§ЕуQзїQN
BCНЛABгкЕуMЃЌЙ§ЕуQзїQN![]() BCЃЌДЙзуЮЊЕуNЃЌСЌНгMQЃЌШєЩшдЫЖЏЪБМфЮЊt(s)(0<t<3)ЃЌНтД№ЯТСаЮЪЬтЃК
BCЃЌДЙзуЮЊЕуNЃЌСЌНгMQЃЌШєЩшдЫЖЏЪБМфЮЊt(s)(0<t<3)ЃЌНтД№ЯТСаЮЪЬтЃК
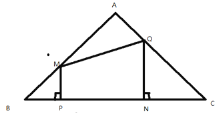
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌЕуMЪЧБпABжаЕу?
ЃЈ2ЃЉЩшЫФБпаЮPNQMЕФУцЛ§ЮЊy(cm2)ЃЌЧѓГіyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙSЫФБпаЮPNQM:SЁїABC=4:9?ШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЃЈ4ЃЉЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЫФБпаЮPNQMЮЊе§ЗНаЮ?ШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉЕБtЮЊ![]() sЪБЃЌЕуMЪЧABжаЕуЃЛ
sЪБЃЌЕуMЪЧABжаЕуЃЛ
ЃЈ2ЃЉyгыtЕФКЏЪ§ЙиЯЕЪНЪЧy![]()
ЃЈ3ЃЉtЕФжЕЮЊ![]() sЃЛ
sЃЛ
ЃЈ4ЃЉВЛДцдкЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіBDЃН3ЃЌИљОн![]() ЃЌМДПЩЧѓГіЪБМфtЃЛ
ЃЌМДПЩЧѓГіЪБМфtЃЛ
ЃЈ2ЃЉЯШХаЖЯГіЁїMBPЁзЁїABDЃЌНјЖјЕУГіMPЃЌЭЌРэБэЪОГіQNКЭCNЃЌШЛКѓРћгУЬнаЮУцЛ§ЙЋЪННјааМЦЫуМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉжаЫљЧѓЃЌНсКЯУцЛ§жЎМфЕФЙиЯЕНЈСЂЗНГЬМДПЩЕУГіНсТлЃЛ
ЃЈ4ЃЉМйЩшДцдкЃЌЯШРћгУPMЃНQNЧѓГіtЃЌНјЖјЧѓГіPMЃЌPNЃЌХаЖЯГіPMЁйPNМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЙ§ЕуAзїADЁЭBCгкЕуDЃЌ
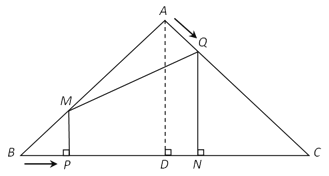
ЁпPMЁЭBCЃЌ
ЁрPMЁЮADЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЕуMЪЧABжаЕу
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпAB = ACЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпBP=tЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
МДЕБtЮЊ![]() sЪБЃЌЕуMЪЧABжаЕуЃЛ
sЪБЃЌЕуMЪЧABжаЕуЃЛ
ЃЈ2ЃЉЙ§ЕуAзїADЁЭBCгкЕуDЃЌ
ЁпPMЁЮADЃЌ
ЁрЁїMBPЁзЁїABDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЭЌРэЃЌЁїQCNЁзЁїACDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрy =SЫФБпаЮPNQM=![]() ЃЌ
ЃЌ
МДyгыtЕФКЏЪ§ЙиЯЕЪНЪЧy![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєSЫФБпаЮPNQM ЃКSЁїABCЃН4ЃК9ЃЌдђy=![]() SЁїABCЃЌ
SЁїABCЃЌ
ЁпSЁїABC=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЁрtЕФжЕЮЊ![]() sЃЛ
sЃЛ
ЃЈ3ЃЉШєЫФБпаЮPNQMЮЊе§ЗНаЮЃЌдђашТњзуPM = QNЃЌPM = PNЃЌ
ЕБPM = QNЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌPM =
ЪБЃЌPM =![]() ЃЌPN=
ЃЌPN=![]() ЃЌ
ЃЌ
ЁрPMЁйPNЃЌ
ЁрВЛДцдкЃЎ

 ШЋФмВтПивЛБОКУОэЯЕСаД№АИ
ШЋФмВтПивЛБОКУОэЯЕСаД№АИ