题目内容
根据下列条件,分别求出二次函数的表达式.
(1)已知二次函数的图象经过点(0,2)、(1,1)、(3,5);
(2)已知二次函数图象的顶点为(-1,2),且过点(2,1);
(3)已知二次函数图象与x轴交于点M(-1,0)、N(2,0),且经过点(1,2).
(1)已知二次函数的图象经过点(0,2)、(1,1)、(3,5);
(2)已知二次函数图象的顶点为(-1,2),且过点(2,1);
(3)已知二次函数图象与x轴交于点M(-1,0)、N(2,0),且经过点(1,2).
考点:待定系数法求二次函数解析式
专题:
分析:(1)设二次函数解析式为y=ax2+bx+c,把三点坐标代入求出a,b,c的值,即可确定出二次函数解析式;
(2)直接利用顶点式假设出二次函数解析式,进而代入(-3,-2)求出即可;
(3)利用交点式y=a(x-x1)(x-x2),把M(-1,0)、N(2,0)及点(1,2)代入求解析式.
(2)直接利用顶点式假设出二次函数解析式,进而代入(-3,-2)求出即可;
(3)利用交点式y=a(x-x1)(x-x2),把M(-1,0)、N(2,0)及点(1,2)代入求解析式.
解答:解:(1)设二次函数解析式为y=ax2+bx+c,
把三点坐标代入得:
,
解得:a=1,b=-2,c=2.
则二次函数解析式为y=x2-2x+2.
(2)设解析式为:y=a(x+1)2+2,
将(2,1)代入得出:1=a(2+1)2+2,
解得:a=-
.
故这个二次函数的解析式为:y=-
(x+1)2+2.
(3)设函数的解析式为y=a(x+1)(x-2),
把(1,2)代入得:a=-1,
∴函数解析式为y=-(x+1)(x-2),
即y=-x2+x+2.
把三点坐标代入得:
|
解得:a=1,b=-2,c=2.
则二次函数解析式为y=x2-2x+2.
(2)设解析式为:y=a(x+1)2+2,
将(2,1)代入得出:1=a(2+1)2+2,
解得:a=-
| 1 |
| 9 |
故这个二次函数的解析式为:y=-
| 1 |
| 9 |
(3)设函数的解析式为y=a(x+1)(x-2),
把(1,2)代入得:a=-1,
∴函数解析式为y=-(x+1)(x-2),
即y=-x2+x+2.
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组的解法等知识,难度不大.

练习册系列答案
相关题目
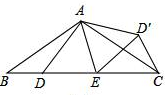 如图,在△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E,DE′=DE.
如图,在△ABC中,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′,连结D′E,DE′=DE.