题目内容
4.请写出一个根为$\sqrt{2}$,另一根满足-1<x<1的一元二次方程是x2-$\sqrt{2}$x=0.分析 由于另一根满足-1<x<1,则可设另一个为0,再计算$\sqrt{2}$+0=1,$\sqrt{2}$×0=0,然后根据根与系数的关系写出满足条件的一元二次方程.
解答 解:设另一个为0,
因为$\sqrt{2}$+0=1,$\sqrt{2}$×0=0,
所以以0和$\sqrt{2}$为根的一元二次方程可为x2-$\sqrt{2}$x=0.
故答案为x2-$\sqrt{2}$x=0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
12.某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为x,则根据题意列方程为( )
| A. | 200(1+x)2=1000 | B. | 200+200(1+x)2=1000 | ||
| C. | 200(1+x)3=1000 | D. | 200+200(1+x)+200(1+x)2=1000 |
19.抛物线y=x2-x-1与坐标轴的交点个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
9.下列计算正确的是( )
| A. | 7a+a=7a2 | B. | 7y-5y=2 | C. | 4x2y-3yx2=x2y | D. | 4a+b=5ab |
16. 将图中的图案以圆心为中心,旋转180°后得到的图案是( )
将图中的图案以圆心为中心,旋转180°后得到的图案是( )
 将图中的图案以圆心为中心,旋转180°后得到的图案是( )
将图中的图案以圆心为中心,旋转180°后得到的图案是( )| A. |  | B. |  | C. |  | D. |  |
13.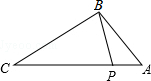 如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
 如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | AB2=AP•AC | D. | AB•BC=AC•BP |