题目内容
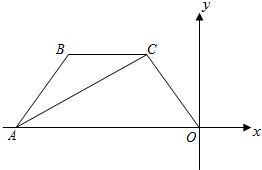 如图,在平面直角坐标系中,四边形OABC的顶点A在x轴上,OA∥BC,∠BAC=∠BCA,OA=4,BC=2,点C的坐标为(-1,
如图,在平面直角坐标系中,四边形OABC的顶点A在x轴上,OA∥BC,∠BAC=∠BCA,OA=4,BC=2,点C的坐标为(-1,| 3 |
(1)写出点A和点B的坐标;
(2)证明:∠BAC=∠OAC;
(3)若∠BAO+∠AOC=120°,∠CAO与∠AOC互余,求∠BAC与∠AOC的度数.
考点:坐标与图形性质,解二元一次方程组,余角和补角,平行线的性质
专题:
分析:(1)由OA=4及点A在x轴负半轴上可得点A的坐标,由OA∥BC可知B、C两点纵坐标相同,由BC=2,点C的坐标为(-1,
)可得点B的坐标;
(2)由两直线平行,内错角相等可得∠BCA=∠OAC,由∠BAC=∠BCA,等量代换可得∠BAC=∠OAC;
(3)设∠BAC=x,∠AOC=y,根据∠AOC+∠BAO=120°,∠CAO与∠AOC互余,列出方程组
,解方程组即可.
| 3 |
(2)由两直线平行,内错角相等可得∠BCA=∠OAC,由∠BAC=∠BCA,等量代换可得∠BAC=∠OAC;
(3)设∠BAC=x,∠AOC=y,根据∠AOC+∠BAO=120°,∠CAO与∠AOC互余,列出方程组
|
解答:解:(1)∵OA=4,点A在x轴负半轴上,
∴A(-4,0).
∵OA∥BC,
∴B、C两点纵坐标相同,
∵BC=2,C(-1,
),
∴B(-3,
);
(2)∵OA∥BC,
∴∠BCA=∠OAC,
又∵∠BAC=∠BCA,
∴∠BAC=∠OAC;
(3)设∠BAC=x,∠AOC=y,
∵∠AOC+∠BAO=120°,∠CAO与∠AOC互余,
∴
,解得
,
即∠BAC=30°,∠AOC=60°.
∴A(-4,0).
∵OA∥BC,
∴B、C两点纵坐标相同,
∵BC=2,C(-1,
| 3 |
∴B(-3,
| 3 |
(2)∵OA∥BC,
∴∠BCA=∠OAC,
又∵∠BAC=∠BCA,
∴∠BAC=∠OAC;
(3)设∠BAC=x,∠AOC=y,
∵∠AOC+∠BAO=120°,∠CAO与∠AOC互余,
∴
|
|
即∠BAC=30°,∠AOC=60°.
点评:本题考查了坐标与图形性质,平行线的性质,余角的性质,解二元一次方程组,难度适中.

练习册系列答案
相关题目
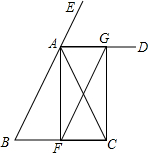 如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.
如图,∠CAE是△ABC的外角,AD平分∠EAC,且AD∥BC.过点C作CG⊥AD,垂足为G,AF是BC边上的中线,连接FG.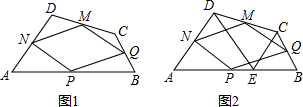
 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.