题目内容
4.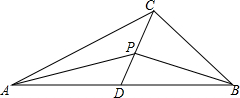 如图,设一个三角形的三边分别是3,1-3m,8.
如图,设一个三角形的三边分别是3,1-3m,8.(1)求m的取值范围;
(2)是否存在整数m使三角形的周长为偶数?若存在,求出三角形的周长;若不存在,说明理由;
(3)如图,在(2)的条件下,当AB=8,AC=1-3m,BC=3时,若D是AB的中点,连CD,P是CD上动点(不与C,D重合,当P在线段CD上运动时,有两个式子):①$\frac{{S}_{△ABC}}{{S}_{△APC}+{S}_{△BPD}}$;②$\frac{PA+PB}{AB}$,其中有一个的值不变,另一个的值改变.问题:
A.请判断出谁不变,谁改变;
B.若不变的求出其值,若改变的求出变化的范围.
分析 (1)利用三角形三边关系列出不等式组求解即可,
(2)利用m的取值范围求出m为整数的值,即可求出三角形的周长,
(3)点D是AB的中点,设点A到CD的距离为h,则点B到CD的距离为h,可得S△APC与S△BPD,得邮S△APC+S△BPD与S△ABC的关系,即可得出$\frac{{S}_{△ABC}}{{S}_{△APC}+{S}_{△BPD}}$的值,由AB=8,AC=7,BC=3,结合由三角形两边之和大于第三边性质可以知道1<$\frac{PA+PB}{AB}$<$\frac{5}{4}$.
解答 解:(1)由三角形三边关系可得$\left\{\begin{array}{l}{3+1-3m>8}\\{3+8>1-3m}\end{array}\right.$,解得-10/3<m<-4/3;
(2)∵-10/3<m<-4/3;
∴m为整数的时候取值只可为-2,
∴1-3m=7,
∴周长是3+7+8=18;
(3)∵点D是AB的中点,设点A到CD的距离为h,则点B到CD的距离为h,
∴S△APC=$\frac{1}{2}$PC•h,S△BPD=$\frac{1}{2}$PD•h,
∴S△APC+S△BPD=$\frac{1}{2}$(PC+PD)h=$\frac{1}{2}$CD•h,
∵S△ABC=$\frac{1}{2}$CD•h+$\frac{1}{2}$CD•h=CD•h,
∴$\frac{{S}_{△ABC}}{{S}_{△APC}+{S}_{△BPD}}$=$\frac{1}{\frac{1}{2}}$=2
∴①不改变;
∵AB=8,AC=7,BC=3
∴由三角形两边之和大于第三边性质可以知道AB<AP+PB<AC+CB,即8<AP+PB<10,
∴1<$\frac{PA+PB}{AB}$<$\frac{10}{8}$,即1<$\frac{PA+PB}{AB}$<$\frac{5}{4}$.
∴②改变.
点评 本题主要考查了面积及等积变换,涉及三角形三角性质,解不等式及等积变换等知识,解题的关键是等积变换及三角形三边关系的灵活运用.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案 将一张等宽的纸条按图中方式折叠,若∠1=40°,则∠2的度数为( )
将一张等宽的纸条按图中方式折叠,若∠1=40°,则∠2的度数为( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
| A. | (1,0) | B. | (2,0) | C. | (3,0) | D. | (4,0) |
 一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的侧面积为15π.
一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的侧面积为15π.