题目内容
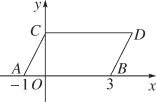
【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将A，B两点向右平移1个单位，再向上平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD.
(1)求点C，D的坐标；
(2)若点P在直线BD上运动，连接PC，PO.
①若点P在线段BD上(不与B，D重合)时，求S△CDP＋S△BOP的取值范围；
②若点P在直线BD上运动，试探索∠CPO，∠DCP，∠BOP的关系，并证明你的结论．
【答案】（1）由平移可知点C的坐标为(0，2)，点D的坐标为(4，2)；（2）①3＜S△CDP＋S△BOP＜4；②当点
在线段
上时，
；当点在线段的延长线上时，
；当点在线段
的延长线上时，
.
【解析】
（1）根据向右平移横坐标加，向上平移纵坐标加求出
、
的坐标即可；
（2）①设点的纵坐标为
，将
与
的面积表示出来，从而得到
，根据题可知
，即可得到
的范围；
②分三种情况，根据平移的性质可得
，再过点作
，根据平行公理可得
，然后根据两直线平行，内错角相等可得
，
即可得到结论.
（1）由平移可知点的坐标为
，点的坐标为
；
（2）①设点的纵坐标为，
点在线段上运动，点
、的坐标分别为
，，易知，
，
，
轴，
，
，
，
，
，
；
②当点在线段上时，如图1
由平移的性质得，，
过点作，则，
，，
，
当点在线段的延长线上时，如图2，
由平移的性质得，，
点作，则，
，，
，
当点在线段的延长线上时，如图3，
同（2）的方法得出.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
