题目内容
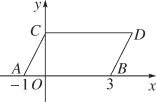
【题目】如图1,在平面直角坐标系中,![]() ,过C作
,过C作![]() 轴于B.
轴于B.
(1)三角形ABC的面积![]() _____________;
_____________;
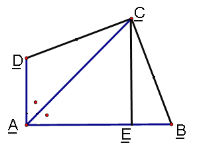
(2)如图2,过B作![]() 交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)点P在y轴上,使得三角形ABC和三角形ACP的面积相等,直接写出P点坐标.



【答案】(1)4;(2)45°;(3)P(0,-1)或(0,3)
【解析】
(1)根据点的坐标,可以得到AB、BC的长度,然后计算面积;
(2)过E作EF∥AC,根据平行线性质得BD∥AC∥EF,且∠3=![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4=![]() ∠ODB=∠2,所以∠AED=∠1+∠2=
∠ODB=∠2,所以∠AED=∠1+∠2=![]() (∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90°,代入计算即可.
(∠CAB+∠ODB);然后把∠CAB+∠ODB=∠5+∠6=90°,代入计算即可.
(3)分类讨论:设P(0,t),分P在y轴正半轴上时或在y轴负半轴时,过P作MN∥x轴,AN∥y轴,BM∥y轴,利用S△APC=S梯形MNAC-S△ANP-S△CMP=4,可得到关于t的方程,再解方程求出t即可;
解:(1)∵![]() ,
,
∴B(2,0),
∴AB=4,BC=2,
∴三角形ABC的面积![]()
![]() .
.
故答案为:4.
(2)解:如图,过E作![]()
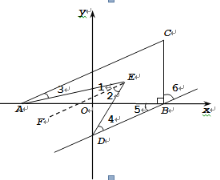
![]() 轴,
轴,![]() ,
,
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∵AE,DE分别平分![]()
∴![]()
∴![]() ;
;
(3)设P(0,t),过P作MN∥x轴,AN∥y轴,BM∥y轴,
①当P在y轴正半轴上时,如图1,
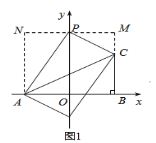
∵![]()
∴![]() ×4×(t+t-2)-
×4×(t+t-2)- ![]() ×2t-
×2t- ![]() ×2×(t-2)=4,
×2×(t-2)=4,
解得:t=3,
∴P点的坐标为:(0,3);
②当P在y轴负半轴上时,如图2,
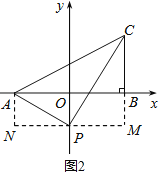
∵![]()
∴![]() ×4(-t+2-t)+
×4(-t+2-t)+![]() ×2t-
×2t-![]() ×2(2-t)=4,
×2(2-t)=4,
解得:t=-1,
∴P点的坐标为:(0,-1);
∴综上所述,P点坐标为:(0,-1)或(0,3).

练习册系列答案
相关题目