题目内容
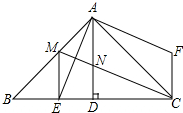
20. 如图,在等边三角形ABC中,D为边AC的中点,DG∥BC交AB于点G,E为BC延长线上的一点,且∠EDF=120°,DF交AB于点F.
如图,在等边三角形ABC中,D为边AC的中点,DG∥BC交AB于点G,E为BC延长线上的一点,且∠EDF=120°,DF交AB于点F.(1)求证:△CDE≌△GDF;
(2)求证:AF-CE=$\frac{1}{2}$AB;
(3)连接BD,已知AB=8,DF=2$\sqrt{6}$,求∠BDF的度数.
分析 (1)根据等边三角形的性质得出AB=AC=BC,∠A=∠B=∠ACB=60°,求出DG=DC,∠GDF=∠CDE,根据ASA推出△DCE≌△DGF即可;
(2)根据全等三角形的性质得出CE=GF,即可得出答案;
(3)过D作DH⊥BC于H,于是得到三角形HDE是直角三角形,求得∠HDC=30°,根据全等三角形的性质得到DE=DF=2$\sqrt{6}$,解直三角形得到CD=$\frac{1}{2}$AC=$\frac{1}{2}$AB=4,根据勾股定理得到DH=2$\sqrt{3}$,证得HE=$\sqrt{D{E}^{2}-D{H}^{2}}$=2$\sqrt{3}$=DH,得到∠HDE=∠E=45°,即可得到结论.
解答 证明:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠A=∠B=∠ACB=60°,
∵D为AC的中点,
∴AD=DC=$\frac{1}{2}$AC,
∵DG∥BC,
∴∠AGD=∠B=∠ADG=∠C=60°,
∴△ADG为等边三角形.
∴AG=DG=AD,
∴DG=DC,
∵∠EDF=∠GDC=120°,
∴∠GDF=∠CDE,
在△DCE和△DGF中,
$\left\{\begin{array}{l}{∠DGF=∠DCE}\\{DC=DG}\\{∠GDF=∠CDE}\end{array}\right.$,
∴△DCE≌△DGF;
(2)∵△DCE≌△DGF,
∴CE=GF,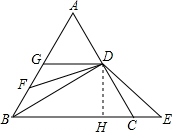
∴AF-CE=AF-GF=AG=$\frac{1}{2}$AB;
(3)过D作DH⊥BC于H,则三角形HDE是直角三角形,且∠HDC=30°,
∵△DCE≌△DGF,
∴DE=DF=2$\sqrt{6}$,
在Rt△HDC中,∵∠ACH=60°,
CD=$\frac{1}{2}$AC=$\frac{1}{2}$AB=4,
∴DH=2$\sqrt{3}$,则HE=$\sqrt{D{E}^{2}-D{H}^{2}}$=2$\sqrt{3}$=DH,
∴∠HDE=∠E=45°,
∴∠CDE=∠HDE-∠HDC=15°,
∴∠GDF=15°,
∴∠BDF=90°-60°-15°=15°.
点评 本题考查了等边三角形的性质,全等三角形的性质和判定的应用,解此题的关键是求出△DCE≌△DGF,注意:等边三角形的三边都相等,等边三角形的每个角都等于60°.

| A. | $\frac{4{y}^{2}}{{x}^{2}}$ | B. | $\frac{2xy}{{x}^{2}}$ | C. | $\frac{y}{2x}$ | D. | -$\frac{-2y}{-x}$ |
| A. |  -3.5 | B. |  -0.6 | C. |  +0.7 | D. |  +2.5 |
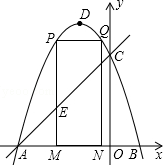 如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.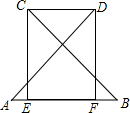 如图,已知:∠A=∠B,CE⊥AB,DF⊥AB,垂足分别为E,F,AD=BC.求证:AE=BF.
如图,已知:∠A=∠B,CE⊥AB,DF⊥AB,垂足分别为E,F,AD=BC.求证:AE=BF.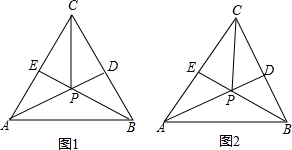
 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.