Question

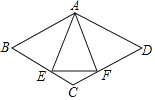
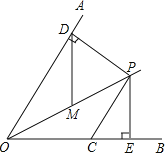
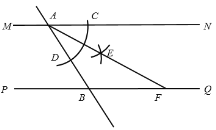
【题目】如图，直线，直线分别与、相交于点、．小亮同学利用尺规按以下步骤作图：①以点为圆心，以任意长为半径作弧交于点，交于点；②分别以、为圆心，以大于长为半径作弧，两弧在内交于点；③做射线交于点．若，，则的内切圆半径长等于__________．

Answer 1

【答案】

【解析】

根据题中尺规作图方法可知AF为∠BAN的角平分线，根据已知条件可知△ABF是以顶角为120°的等腰三角形，再根据内切圆半径与三角形面积的关系即可求出内切圆半径．

解：由题意可知，AF为∠BAN的角平分线，

∵，，

∴∠BAN=60°，∠ABF=120°，

∵AF为∠BAN的角平分线

∴∠BAF=∠NAF=30°，

∴∠AFB=30°

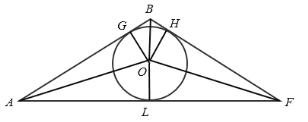
∴△ABF是以顶角为120°的等腰三角形，如下图所示

设圆O为△ABF的内切圆，过点O作OG⊥AB于点G，OH⊥AB于点H，OL⊥AF于点L，连接OA，OB，OF，设内切圆半径为r，则OG=OH=OL=r

∵

∴AF=AB=2，AF=2，BL=1

由等面积法可知：，

即

解得：

故答案为：．