Question

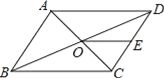
【题目】如图，已知OP平分∠AOB，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．CP＝，PD＝6．如果点M是OP的中点，则DM的长是_____．

Answer 1

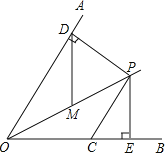
【答案】5．

【解析】

由角平分线的性质得出∠AOP=∠BOP，PC=PD=6，∠PDO=∠PEO=90°，由勾股定理得出，由平行线的性质得出∠OPC=∠AOP，得出∠OPC=∠BOP，证出，得出OE=CE+CO=8，由勾股定理求出，再由直角三角形斜边上的中线性质即可得出答案．

∵OP平分∠AOB，PD⊥OA于点D，PE⊥OB于点E，

∴∠AOP＝∠BOP，PC＝PD＝6，∠PDO＝∠PEO＝90°，

∴，

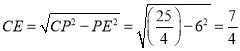∵CP∥OA，

∴∠OPC＝∠AOP，

∴∠OPC＝∠BOP，

∴，

∴，

∴，

在Rt△OPD中，点M是OP的中点，

∴；

故答案为：5．