Question

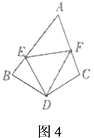
【题目】如图，在菱形ABCD中，点E，F分别在BC，CD上，且CE＝CF，

（1）求证△ABE≌△ADF．

（2）若∠B＝50°，AE⊥BC，求∠AEF的度数．

Answer 1

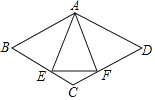
【答案】（1）见解析；（2）∠AEF＝65°

【解析】

（1）由“SAS”可证△ABE≌△ADF；

（2）由菱形的性质可求∠C＝110°，由余角的性质可求∠CEF的值，即可求∠AEF的值．

证明：（1）∵四边形ABCD是菱形，

∴AB＝AD＝BC＝CD，∠B＝∠D，AB∥CD．

∵CE＝CF，

∴BE＝DF，且∠B＝∠D，AB＝AD，

∴△ABE≌△ADF（SAS）；

（2）∵AB∥CD，

∴∠B+∠C＝180°，且∠B＝50°，

∴∠C＝130°，且CE＝CF，

∴∠CEF＝25°．

∵AE⊥BC，

∴∠AEF＝90°﹣25°＝65°．