题目内容
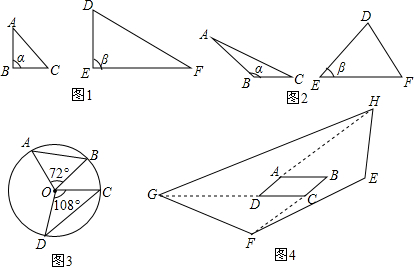
10.阅读理解:两个三角形中有一个角相等或互补,我们称这两个三角形是共角三角形,这个角称为对应角.
(1)根据上述定义,判断下列结论,正确的打“√”,错误的打“×”.
①三角形一条中线分成的两个三角形是共角三角形.对
②两个等腰三角形是共角三角形.错
【探究】
(2)如图,在△ABC与△DEF中,设∠ABC=α,∠DEF=β
①当α=β=90° 时,显然可知:$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=$\frac{AB•BC}{DE•EF}$
②当α=β≠90°时,亦可容易证明:$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=$\frac{AB•BC}{DE•EF}$
③如图2,当α+β=180°(α≠β)时,上述的结论是否还能成立,若成立,请证明;若不成立,请举反例说明.
【应用】
(3)如图3,⊙O中的弦AB、CD所对的圆心角分别是72°、108°,记△OAB与△OCD的面积分别为S1,S2,请写出S1与S2满足的数量关系S1=S2.
(4)如图4,?ABCD的面积为2,延长□ABCD的各边,使BE=AB,CF=2BC,DG=2CD,AH=3AD,则四边形EFGH的面积为25.
分析 (1)①②根据共角三角形的定义,可得答案;
(2)根据同角的补角相等,可得:∠ABM=∠E,根据相似三角形的判定,可得△ABM∽△DEN,根据相似三角形的性质,可得对应边的比相等,可得证明的结论;
(3)根据共角三角形面积的关系,可得答案;
(4)根据共角三角形面积的关系,可得共角三角形的面积,根据面积的和差,可得答案..
解答 解:(1)根据共角三角形的定义可知①对 ②错;
故答案为对,错.
(2)③证明:如图2中,过A作AM⊥BC交BC的延长线于点M、过D作DN⊥EF于点N,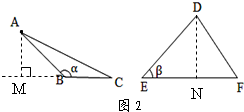
∴∠AMB=∠DNE=90°
又∵∠ABM+α=β+α=180°
∴∠ABM=β
即:∠ABM=∠E
∴△ABM∽△DEN
∴$\frac{AM}{DN}$=$\frac{AB}{DE}$,
∴$\frac{{S}_{△ABC}}{{S}_{△DEF}}$=$\frac{\frac{1}{2}AM•BC}{\frac{1}{2}DN•EF}$=$\frac{AM}{DN}$•$\frac{BC}{EF}$=$\frac{AB}{DE}$•$\frac{BC}{EF}$=$\frac{AB•BC}{DE•EF}$;
(3)如图3中,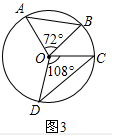
∵△OAB与△OCD是共角三角形,OA=OB=OC=OD,
∴$\frac{{S}_{△OAB}}{{S}_{△OCD}}$=$\frac{{S}_{1}}{{S}_{2}}$=$\frac{OA•OB}{OC•OD}$=1,
∴S1=S2;
故答案为:S1=S2.
(4)如图4中,连接AC、BD.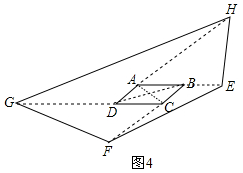
四边形ABCD的面积为2,
S△ABC=S△ADC=S△BAD=S△BCD=1,
使BE=AB,CF=2BC,DG=2CD,AH=3AD,
由共角三角形的面积比等于对应角两边的乘积之比得
$\frac{{S}_{△BEF}}{{S}_{△ABC}}$=$\frac{BE•EF}{AB•BC}$=$\frac{AB•3BC}{AB•BC}$=3,S△BEF=3,
$\frac{{S}_{△GCF}}{{S}_{△BCD}}$=$\frac{CG•CF}{CB•CD}$=$\frac{3CD•2BC}{CD•BC}$=6,S△GCF=6,
$\frac{{S}_{△HDG}}{{S}_{△ADC}}$=$\frac{DG•DH}{DA•DC}$=$\frac{2CD•4DA}{CD•DA}$=8,S△DGH=8,
$\frac{{S}_{△AHE}}{{S}_{△ADB}}$=$\frac{AH•AE}{AD•AB}$ $\frac{3AD•2AB}{AD•AB}$═6,S△AHE=6,
SEFGH=S△BEF+S△GCF+S△DGH+S△AHE+SABCD
=3+6+8+6+2=25,
故答案为25.
点评 本题考查了圆的综合题,共角三角形的面积之间的关系是解题关键.

 如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横竖彩条的宽度比为2:1,如果要使彩条所占面积是图案面积的$\frac{19}{75}$,则竖彩条宽度为( )
如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横竖彩条的宽度比为2:1,如果要使彩条所占面积是图案面积的$\frac{19}{75}$,则竖彩条宽度为( )| A. | 1cm | B. | 1.5cm | C. | 2cm | D. | 2.5cm |
 如图,△ABC为等边三角形,且BM=CN,AM与BN相交于点P,则∠APN=( )
如图,△ABC为等边三角形,且BM=CN,AM与BN相交于点P,则∠APN=( )| A. | 70° | B. | 60° | C. | 50° | D. | 大小不确定 |
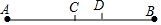 如图,线段AB=8cm,点C是AB的中点,点D在CB上且DC=1.5cm,求线段BD的长度.
如图,线段AB=8cm,点C是AB的中点,点D在CB上且DC=1.5cm,求线段BD的长度.
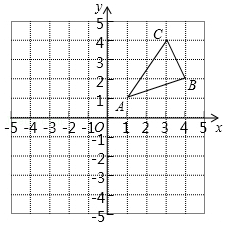 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).