题目内容
已知关于x的方程x2-2x+k-1=0有两个不相等的实数根，则k的取值范围是 ．
考点：根的判别式
专题：计算题
分析：根据判别式的意义得到△=（-2）2-4×1×（k-1）＞0，然后解不等式即可．
解答：解：根据题意得△=（-2）2-4×1×（k-1）＞0，
解得k＜2．
故答案为k＜2．
解得k＜2．
故答案为k＜2．
点评：本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．
练习册系列答案
相关题目
我们给出如下定义：点P是等边△ABC内一点，连结PA，PB，PC，我们称以PA，PB，PC为边构成的新三角形为原三角形的“联谊三角形”．
利用图14×4正方形网格，作出面积为5平方单位的正方形，并在图2数轴上作出如果a与3互为相反数，那么a等于（ ）
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
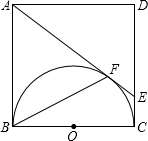如图，正方形ABCD的边长为4cm，以正方形的一边BC为直径在正方形ABCD内作半圆，过A点作半圆的切线，与半圆相切于点F，与DC相交于点E，求BF的长．